题目内容
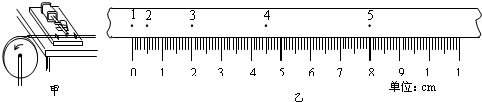
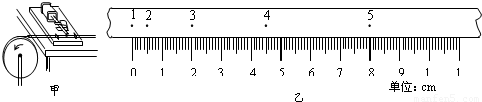
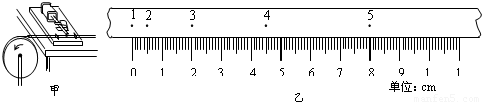
A．一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，某同学用打点计时器来研究它由静止开始转动的情况．如图甲所示，纸带固定在待测圆盘的侧面上，使得圆盘转动时，纸带可以卷在圆盘侧面上．先让打点计时器开始打点，然后使圆盘由静止开始转动，得到如图乙的一段纸带，纸带上每两个相邻计数点间均有四个点未标出．已知圆盘半径r=5.50×10-2m，交流电频率是50Hz，公式v=ω-r表示线速度和角速度的瞬时对应关系，则研究这段纸带会发现，在0-0.4秒这段时间内，圆盘的角速度变化特点是______；如果用类似于研究匀加速度运动的方法研究圆盘这段时间内的转动，那么描述圆盘角速度变化快慢的角加速度为______．
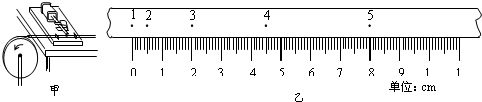
连续的四段间隔为：0.5cm，1.5cm，2.5cm，3.5cm；
由于连续两端位移差△x=1.0cm是恒定的，故是匀加速曲线运动；
根据公式△x=aT2得到：a=
=
=1m/s2；
角加速度β=
=
=
=
≈18.2m/s2；
故答案为：随时间均匀变大，18.2m/s2．
由于连续两端位移差△x=1.0cm是恒定的，故是匀加速曲线运动；
根据公式△x=aT2得到：a=
| △v |
| T2 |
| 0.01m |
| (0.1s)2 |
角加速度β=
| △ω |
| △t |
| △v |
| r?△t |
| a |
| r |
| 1 |
| 5.50×10-2 |
故答案为：随时间均匀变大，18.2m/s2．
练习册系列答案
小学课时作业全通练案系列答案
相关题目
