题目内容
(2009?淮南三模)一个有一定厚度的圆盘,可以绕通过其中心并垂直于盘面的水平轴转动,将圆盘加速转动时角速度的增加量△ω与对应时间△t的比值定义为角加速度β(即β户等).我们用电磁打点计时器、米尺、纸带、复写纸来完成下述实验:

①如图甲所示,将打点计时器固定在桌面上,使纸带的一端穿过打点计时器的限位孔,然后固定在圆盘的侧面,当圆盘转动时,纸带可以卷在圆盘侧面上;②接通电源.打点计时器开始打点,启动控制装置使圆盘匀加速转动;③经过一段时间,停止转动和打点,取下纸带进行测量.(打点计时器所接的交变电流的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出,计算时不考虑纸带卷在圆盘侧面时引起圆盘半径的变化)
(1)如图乙所示,圆盘的半径r=
(2)由图丙可知,打下计数点D时,纸带运动的速度大小为
(3)纸带运动的加速度大小为
[(2)、(3)两问中的结果均保留两位有效数字].

①如图甲所示,将打点计时器固定在桌面上,使纸带的一端穿过打点计时器的限位孔,然后固定在圆盘的侧面,当圆盘转动时,纸带可以卷在圆盘侧面上;②接通电源.打点计时器开始打点,启动控制装置使圆盘匀加速转动;③经过一段时间,停止转动和打点,取下纸带进行测量.(打点计时器所接的交变电流的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出,计算时不考虑纸带卷在圆盘侧面时引起圆盘半径的变化)
(1)如图乙所示,圆盘的半径r=
6.00
6.00
cm(2)由图丙可知,打下计数点D时,纸带运动的速度大小为
0.39
0.39
m?s-1,此时圆盘转动的角速度为6.5
6.5
rad?s-1.(3)纸带运动的加速度大小为
0.59
0.59
m?s-2,圆盘转动的角加速度大小为9.8
9.8
rad?s-2.[(2)、(3)两问中的结果均保留两位有效数字].
分析:(1)根据米尺读出圆盘的直径,再求出半径
(2)根据平均速度等于中间时刻瞬时速度求出D点的瞬时速度,然后根据v=ωr求解角速度;
(3)用逐差法求解出加速度,再根据加速度等于角加速度与半径的乘积来计算角加速度.
(2)根据平均速度等于中间时刻瞬时速度求出D点的瞬时速度,然后根据v=ωr求解角速度;
(3)用逐差法求解出加速度,再根据加速度等于角加速度与半径的乘积来计算角加速度.
解答:解:(1)根据米尺读圆盘的直径是12.00cm,所以圆盘的半径r=6.00 cm.
(2)由于每相邻两个计数点间还有4个点没有画出,所以相邻的计数点间的时间间隔T=0.1s,
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上D点时小车的瞬时速度大小.
vD=
=
=0.39m/s
故ω=
=
=6.5rad/s
(3)设A到B之间的距离为x1,以后各段分别为x2、x3、x4,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对二个加速度取平均值
得:a=
(a1+a2)
即小车运动的加速度计算表达式为:a=
=
=0.59m/s2
由于β=
,ω=
,故角加速度为β=
=
≈9.8rad/s2
故答案为:
(1)6.00; (2)0.39,6.5; (3)0.59,9.8.
(2)由于每相邻两个计数点间还有4个点没有画出,所以相邻的计数点间的时间间隔T=0.1s,
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上D点时小车的瞬时速度大小.
vD=
| xCE |
| 2T |
| (13.19-5.41)×0.01 |
| 2×0.1 |
故ω=
| v |
| r |
| 0.39 |
| 0.06 |
(3)设A到B之间的距离为x1,以后各段分别为x2、x3、x4,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对二个加速度取平均值
得:a=
| 1 |
| 2 |
即小车运动的加速度计算表达式为:a=
| xCE-xAC |
| 4T2 |
| (13.19-5.41)×0.01-5.14×0.01 |
| 4×(0.1)2 |
由于β=
| △? |
| △t |
| v |
| r |
| a |
| r |
| 0.59 |
| 0.06 |
故答案为:
(1)6.00; (2)0.39,6.5; (3)0.59,9.8.
点评:本题根据根据题意中角加速度的定义,同时结合纸带处理中加速度和速度的求法进行分析处理.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2009?淮南三模)在竖直平面内,有根光滑金属杆弯成如图所示形状,相应的曲线方程为y=Acosx,将一个光滑小环套在该金属杆上,并从x=0、y=A处以某一初速度沿杆向+x方向运动.运动过程中( )
(2009?淮南三模)在竖直平面内,有根光滑金属杆弯成如图所示形状,相应的曲线方程为y=Acosx,将一个光滑小环套在该金属杆上,并从x=0、y=A处以某一初速度沿杆向+x方向运动.运动过程中( )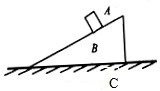 (2009?淮南三模)如图所示,物块A沿楔形块B的斜面下滑时,B相对于水平地面C静止不动,设A、B间的动摩擦因数为μ1,B、C间的动摩擦因数为μ2,则下列说法中不可能的是( )
(2009?淮南三模)如图所示,物块A沿楔形块B的斜面下滑时,B相对于水平地面C静止不动,设A、B间的动摩擦因数为μ1,B、C间的动摩擦因数为μ2,则下列说法中不可能的是( )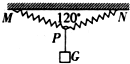 (2009?淮南三模)如图所示,原长为l、劲度系数为k的轻弹簧固定于同一高度的M、N两点,在弹簧的中点P处悬挂一重为G的物体,整个装置处于平衡,此时MP与PN之间的夹角为120°,则此时弹簧的总长度为( )
(2009?淮南三模)如图所示,原长为l、劲度系数为k的轻弹簧固定于同一高度的M、N两点,在弹簧的中点P处悬挂一重为G的物体,整个装置处于平衡,此时MP与PN之间的夹角为120°,则此时弹簧的总长度为( )