题目内容
【题目】如图所示,两个相同的物块A、B用轻绳相连接并放在水平地面上,在方向与水平面成θ=37°角斜向下、大小为100N的恒定拉力F作用下,以大小为v=4m/s的速度向右做匀速直线运动.已知A、B质量均为5kg (g取10m/s2)试求: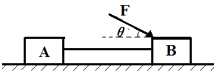
(1)物块与地面之间的动摩擦因数;
(2)剪断轻绳后物块A在水平地面上滑行的时间;
(3)已知轻绳长度L=0.5m,剪断轻绳后,物块A恰好滑至停止时A、B的距离.
【答案】
(1)解:将两物块A、B作为一整体,则:
Fcosθ=μ(Fsinθ+2mg)
代入数据:100×0.8=μ(100×0.6+2×50)
得:μ=0.5
答:物块与地面之间的动摩擦因数为0.5;
(2)解:剪断轻绳后物块A做匀减速运动,则:
μmg=maB
得: ![]()
滑行时间 ![]()
答:剪断轻绳后物块A在水平地面上滑行的时间0.8s;
(3)解:剪断轻绳后物块A做匀减速运动,则A在线断后继续滑行的距离:
![]()
得: ![]()
剪断轻绳断后物块B做匀加速运动,受力分析如图,
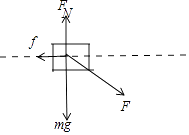
由牛顿第二定律得:
![]()
代入数据: ![]()
得: ![]()
故:线断后到物体A停止滑行间,物体B继续滑行的距离为:
![]()
代入数据: ![]()
所以物块A静止时物块A、B的距离:△x=x′+L﹣x=4.8+0.5﹣1.6=3.7m
答:已知轻绳长度L=0.5m,剪断轻绳后,物块A恰好滑至停止时A、B的距离为3.7m
【解析】将两物块A、B作为一整体进行受力分析,根据共点力的平衡条件求出物体与地面间的动摩擦因数,接着把A隔离出来,对其进行受力分析,再利用牛顿第二定律求出A的加速度大小,根据速度时间关系可以求出A的运动时间;根据牛顿第二定律求出剪断绳子后B物体的加速度,由运动学公式得出A到停止前的位移,并求出此时B的位移,再根据位移关系得出物块A恰好停止时AB的距离。
【考点精析】认真审题,首先需要了解匀变速直线运动的速度、位移、时间的关系(速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值).