题目内容
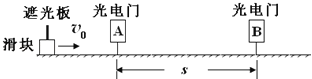
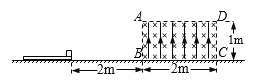
【题目】如图所示,光滑水平地面上方ABCD区域存在互相垂直的匀强磁场和匀强电场,电场强度E=1×106N/C,方向竖直向上,AD距离为2m,CD高度为1m,一厚度不计的绝缘长木板其右端距B点2m,木板质量M=2kg,在木板右端放有一带电量q=+ 1×10-6C的小铁块(可视为质点),其质量m=0.1kg,小铁块与木板间动摩擦因数μ=0.4,现对长木板施加一水平向右的恒力F1=12.4N,作用1s后撤去恒力,g取10m/s2.
(1)求前1s小铁块的加速度大小am,长木板加速度大小aM;
(2)要使小铁块最终回到长木板上且不与长木板发生碰撞,求磁感强度B的最小值;
(3)在t=1s时再给长木板施加一个水平向左的力F2,满足(2)条件下,要使小铁块回到长木板时恰能相对长木板静止,求木板的最小长度(计算过程π取3.14).
【答案】(1)4m/s2;6m/s2;(2)![]() ;(3)6.925m
;(3)6.925m
【解析】试题分析:分别对小木块和长木板受力分析,根据牛顿第二定律求出加速度;由于![]() ,此后小铁块进入复合场做匀速圆周运动,当
,此后小铁块进入复合场做匀速圆周运动,当![]() ,铁块必定会与木板碰撞,当
,铁块必定会与木板碰撞,当![]() 时有可能不会相撞,但B不是最小值,因此要使得小铁块与长木板不发生碰撞,其圆周运动半径r=1m,此时对应的磁场强度最小,根据洛伦兹力提供向心力,求出磁感应强度;撤去F后长木板减速运动,小铁块离开长木板后先在磁场中做匀速圆周运动,出场后竖直上抛,再根据运动学公式即可求出木板的最小长度。
时有可能不会相撞,但B不是最小值,因此要使得小铁块与长木板不发生碰撞,其圆周运动半径r=1m,此时对应的磁场强度最小,根据洛伦兹力提供向心力,求出磁感应强度;撤去F后长木板减速运动,小铁块离开长木板后先在磁场中做匀速圆周运动,出场后竖直上抛,再根据运动学公式即可求出木板的最小长度。
(1)当F作用在长木板上时,对小铁块由牛顿第二定律: ![]() ,
,
解得: ![]()
对长木板: ![]()
代入数据解得: ![]()
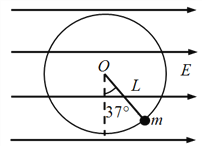
(2)由于![]() ,此后小铁块进入复合场做匀速圆周运动(如图所示),
,此后小铁块进入复合场做匀速圆周运动(如图所示),
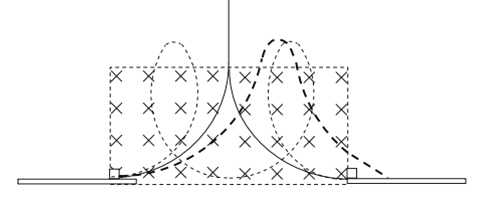
当![]() ,铁块必定会与木板碰撞,当
,铁块必定会与木板碰撞,当![]() 时有可能不会相撞,但B不是最小值,因此要使得小铁块与长木板不发生碰撞,其圆周运动半径r=1m,此时对应的磁场强度最小
时有可能不会相撞,但B不是最小值,因此要使得小铁块与长木板不发生碰撞,其圆周运动半径r=1m,此时对应的磁场强度最小
根据: ![]()
速度关系为: ![]()
联立解得: ![]()
(3)长木板运动1s末位移为: ![]()
速度关系为: ![]()
小铁块运动1s末位移: ![]()
撤去F后长木板减速运动,小铁块离开长木板后先在磁场中做匀速圆周运动,出场后竖直上抛,设小铁块离开长木板的总时间![]()
小铁块在磁场中运动的总时间: ![]()
小铁块出场后上抛与下降的总时间: ![]()
所以: ![]()
若小铁块回到木板时不发生滑动,则木板速度与小铁块相同,此过程木板匀速运动位移为: ![]()
此时小铁块从C点滑上长木板,距木板右端![]()
代入数据得木板的最小长度: ![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案