题目内容
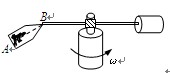
如图，质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a，从距BC高h的A处由静止释放，沿ABC光滑轨道滑下，在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度，悬挂b球的细绳能承受的最大拉力为2.8mg。试问：
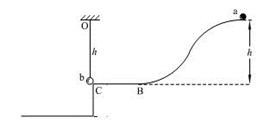
（1）a与b球碰前瞬间，a球的速度多大？
（2）a、b两球碰后，细绳是否会断裂？（要求通过计算回答）
（1）a与b球碰前瞬间，a球的速度多大？
（2）a、b两球碰后，细绳是否会断裂？（要求通过计算回答）
（1）
（2）故绳会断裂
（2）故绳会断裂试题分析：（1）设a球经C点时速度为vc，根据机械能守恒定律：
解得：
，即a与b球碰前的速度为。（2）ab碰撞动量守恒:
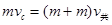
解得：
碰后，ab球一起做圆周运动，在最低点：
解得：
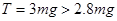，故绳会断裂。点评：本题考察了机械能守恒、动量守恒、平抛运动以及关于向心力的计算．当只有重力（或系统内的弹力）做功时，机械能守恒，减少的重力势能（或弹簧的弹性势能）转化为物体的动能．可用表达式△Ek=mg△h来计算．关于动量守恒定律的应用，首先要确定研究对象，对研究对象进行受力分析，判断是否符合守恒的条件，然后确定正方向，列式求解．对于平抛引动，要把运动分解成水平方向的匀速直线运动和竖直方向的自由落体运动，运行的时间由抛出点的高度决定；水平位移由抛出点的高度和抛出时的速度共同决定．关于向心力的计算，首先要正确的对研究对象进行受力分析，找出沿半径方向上所有力的合力，即为向心力，结合圆周运动的相关公式来解决问题．
练习册系列答案
阅读快车系列答案
相关题目
