题目内容
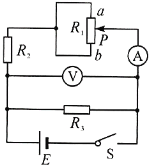
【题目】如图所示,在竖直直角坐标平面xOy区域I(0≤x≤L)和区域Ⅱ内分别存在匀强电场,区域I内电场强度大小为E,方向沿竖直y轴正方向,区域Ⅱ内电场强度大小方向未知,一质量为m、电荷量为q的带正电的小球从坐标原点O以某一初速度沿水平x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达区域Ⅱ右边界的Q点时速度恰好为零,P点的坐标为(L,L).重力加速度为g,求:
(1)带电小球射入电场区域I时的初速度大小.
(2)若区域Ⅱ内电场方向水平,求小球从O到Q电场力做的功。
(3)若区域Ⅱ内场强取最小值,求此最小电场强度和Q点坐标。

【答案】(1) ![]() (2)
(2) ![]() (3)(
(3)(![]() ,
,![]() )
)
【解析】
本题考查带电粒子在匀强电场中的运动。
(1)小球从O到P做类平抛运动,
在x方向匀速:
![]()
在y方向匀加速:
![]()
![]()
解得:
![]()
(2)小球从O到P在x、y方向位移相等,则平均速度相同,如图:

则有:
![]()
即:
![]()
![]()
且vP与x轴夹角正切:
![]()
球从P到Q做匀减速直线运动
若区域II内电场方向水平,一定水平向左,设场强为E′,则有:
![]()
得:
![]()
设区域II的宽度为d,则有:
![]()
则电场力在区域II内做功:
![]()
在区域I内电场力做功:
![]()
所以,小球从O到Q电场力做功为:
![]()
(3)使球从P到Q做匀减速直线运动的场强E′有多种可能,其中最小场强方向与vP垂直斜向左上方,如图,据几何关系,

有:
![]()
得:
![]()
![]()
![]()
从P到Q有:
![]()
![]()
由几何关系有:
![]()
![]()
![]()
∴Q点横坐标:
![]()
Q点纵坐标:
![]()
即:
Q(![]() ,
,![]() )
)

练习册系列答案
相关题目