题目内容
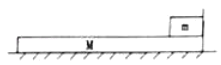
【题目】如图所示,质量为2kg的木板M放置在足够大光滑水平面上,其右端固定一轻质刚性竖直挡板,能承受的最大压力为4N,质量为1kg的可视为质点物块m恰好与竖直挡板接触,已知M、m间动摩擦因数![]() =0.5,假设最大静摩擦力等于滑动摩擦力。初始两物体均静止,某时刻开始M受水平向左力F作用,F与M位移关系为F=3+0.5x,重力加速度g=10m/s2,关于M、m的运动,下列表述正确的是( )
=0.5,假设最大静摩擦力等于滑动摩擦力。初始两物体均静止,某时刻开始M受水平向左力F作用,F与M位移关系为F=3+0.5x,重力加速度g=10m/s2,关于M、m的运动,下列表述正确的是( )
A.m的最大加速度为5m/s2
B.m获得的最大速度无法求解
C.当F刚作用时,竖直挡板对m就有弹力作用
D.当M运动位移为24m过程中,F所做的功为216J
【答案】D
【解析】
A.m与木板M之间的最大静摩擦力为
![]() N=5N
N=5N
m受到的向左的力最大为静摩擦力与弹力的和,所以最大加速度为
am=![]() =
=![]() m/s2=9m/s2
m/s2=9m/s2
故A错误;
BC.开始时m与木板一起做加速运动,共同的加速度为
a=![]() =
=![]() =1+
=1+![]() x
x
刚开始时,x=0,则加速度为a0=1m/s2。开始时m受到的摩擦力为
![]() N=1N<5N
N=1N<5N
所以当F刚作用时,竖直挡板对m没有弹力作用;由am=9m/s2和=1+![]() x,可知当m的加速度最大时的位移为xm=48m,根据F的平均值可求出拉力对系统做的功,由动能定理即可求出系统的动能,即
x,可知当m的加速度最大时的位移为xm=48m,根据F的平均值可求出拉力对系统做的功,由动能定理即可求出系统的动能,即
![]()
由此即可求出m的最大速度,故BC错误;
D.当M运动位移为24m时有
F=3+0.5×24N=15N
根据功的公式有
![]()
可知力F做的功等于力在空间的积累效果,由积累的关系可得
W=![]() x=
x=![]() ×24J=216J
×24J=216J
故D正确。
故选D。

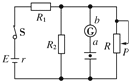
【题目】用下列器材测量电容器的电容:一块多用电表,一台直流稳压电源,一个待测电容器(额定电压16V),定值电阻R1(阻值未知),定值电阻R2=150Ω,电流传感器、数据采集器和计算机,单刀双掷开关S,导线若干.
实验过程如下:
实验次数 | 实验步骤 |
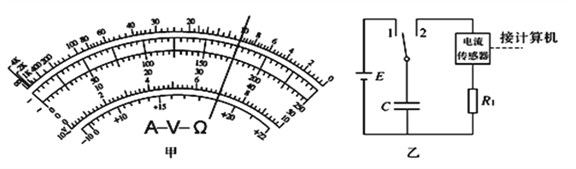
第1次 | ①用多用电表的“×10”挡测量电阻R1,指针偏转如图甲所示. |
②将电阻R1等器材按照图乙正确连接电路,将开关S与1端连接,电源向电容器充电. | |
③将开关S掷向2端,测得电流随时间变化的i﹣t曲线如图丙中的实线a所示. | |
第2次 | ④用电阻R2替换R1,重复上述实验步骤②③,测得电流随时间变化的i﹣t曲线如图丁中的某条虚线所示. |
说明:两次实验中电源输出的直流电压恒定且相同. | |
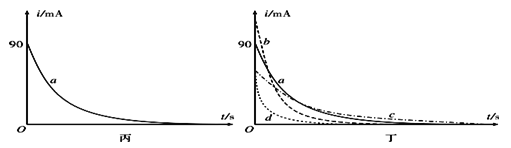
请完成下列问题:
(1)由图甲可知,电阻R1的测量值为______Ω.
(2)第1次实验中,电阻R1两端的最大电压U=___V.利用计算机软件测得i﹣t曲线和两坐标轴所围的面积为42.3mAS,已知电容器放电时其内阻可以忽略不计,则电容器的电容为C=________.
(3)第2次实验中,电流随时间变化的i﹣t曲线应该是图丁中的虚线__(选填“b”、“c”或“d”),判断依据是_________________________________________________.