Question

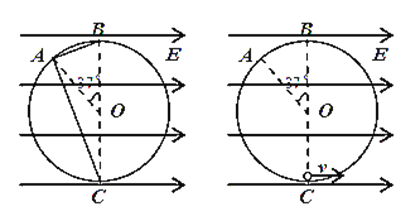
【题目】在竖直平面内有水平向右、电场强度为E＝1×104N/C的匀强电场．在场中有一个半径为R＝2m的光滑圆环，环内有两根光滑的弦AB和AC，A点所在的半径与竖直直径BC成角。质量为0.04kg的带电小球由静止从A点释放,沿弦AB和AC到达圆周的时间相同。现去掉弦AB和AC，给小球一个初速度让小球恰能在竖直平面沿环内做完整圆周运动，不考虑小球运动过程中电量的变化。下列说法正确的是(cos＝0.8，g＝10m/s2)（ ）

A.小球所带电量为q＝3.6×10－5 C

B.小球做圆周运动动能最小值是0.5 J

C.小球做圆周运动经过C点时机械能最小

D.小球做圆周运动的对环的最大压力是3.0N

Answer 1

【答案】BD

【解析】

A．因从A点到E点和C点的运动时间相同，因此可将A点看成在电场和重力场的等效最高点，因此等效重力场的方向为AO方向，因此对小球进行受力分析，小球应带正电，则有

解得小球的带电量为

故A错误；

B．小球做圆周过程中由于重力和电场力都是恒力，所以它们的合力也是恒力，小球的动能、重力势能和电势能之和保持不变，在圆上各点中，小球在等效最高点A的势能（重力势能和电势能之和）最大，则其动能最小，由于小球恰能在竖直平面沿环内做圆周运动，根据牛顿第二定律，在A点其合力作为小球做圆周运动的向心力，有

小球做圆周运动过程中动能最小值为

故B正确；

C．由于总能量保持不变，即

所以小球在圆上最左侧的位置，电势能EPE最大，机械能最小，故C错误；

D．将重力与电场力等效成新的“重力场”，新“重力场”方向与竖直方向成，等效重力为

等效重力加速度为

小球恰好能做圆周运动，在等效最高点A点速度为

在等效最低点小球对环的压力最大，设小球在等效最低点的速度为v，由动能定理得

由牛顿第二定律得

联立解得小球在等效最低点受到的支持力

根据牛顿第三定律知小球做圆周运动的过程中对环的最大压力大小也为3.0N，故D正确。

故选BD。