题目内容
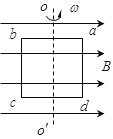
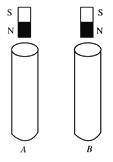
【题目】当金属的温度升高到一定程度时就会向四周发射电子，这种电子叫热电子，通常情况下，热电子的初始速度可以忽略不计。如图所示，相距为L的两块平行金属板M、N接在输出电压恒为U的高压电源E2上，M、N之间的电场近似为匀强电场，a、b、c、d是匀强电场中四个均匀分布的等势面，K是与M板距离很近的灯丝，电源E1给K加热从而产生热电子。电源接通后，电流表的示数稳定为I，已知电子的质量为m、电量为e。求：
（1）电子达到N板瞬间的速度；
（2）电路稳定的某时刻，M、N之间运动的热电子的总动能；
（3）电路稳定的某时刻，c、d两个等势面之间具有的电子数。
【答案】（1）
（2）Ek总=IL
（3）
【解析】（1）电子达到N板的过程中，由动能定理得： 
解得： 
（2）电子从灯丝K出发达到N板的过程中，在电场力的作用下加速，由牛顿定律有： 
，
解得： 
由L＝
at2得：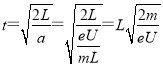 
根据功能关系，在M、N之间运动的热电子的总动能应等于t时间内电流做功的
，
即Ek总=
UIt=
UI（
）=IL
（3）电子从灯丝出发达到c所经历的时间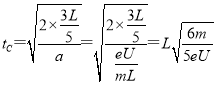
电子从灯丝出发达到d所经历的时间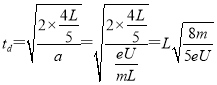
．
c、d两个等势面之间的电子数n=
，
将时间td和tc代入，求出： 
练习册系列答案
相关题目
