题目内容
12.河宽300m,水流速度为3m/s,小船在静水中的速度为5m/s,问:(1)以最短时间渡河,时间为多少?可到达对岸的什么位置?
(2)以最短航程渡河,船头应朝向何处?渡河时间又为多少?(sin37°=0.6 cos37°=0.8)
分析 (1)当船在垂直于河岸方向上的速度最大时,渡河时间最短,即为船头始终指向河对岸时,时间最短.用运动学公式即可得知渡河的最短时间.
(2)船垂直渡河时船的航程最短,此时船头要指向上游,并且沿河岸方向上的分量大小与水流的速度大小相等,对两个速度进行合成,即可求得渡河时间.
解答 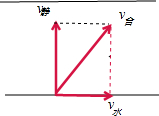 解:(1)要使船到达对岸的时间最短,即为在垂直于河岸的方向上船的速度最大,即为船头应垂直于河岸行驶,如图所示,最短时间为:
解:(1)要使船到达对岸的时间最短,即为在垂直于河岸的方向上船的速度最大,即为船头应垂直于河岸行驶,如图所示,最短时间为:
tmin=$\frac{d}{{v}_{c}}$=$\frac{300}{5}$=60s
此时沿河岸方向的位移x=v水t=3×60m=180m.
航程s=$\sqrt{{d}^{2}+{x}^{2}}$=$\sqrt{30{0}^{2}+18{0}^{2}}$=350m
(2)要使船航程最短,即为让船垂直河岸渡河,船航行的实际速度垂直于河岸,如图所示
设船在静水中的速度方向与河岸间的夹角为θ,船在静水中的速度沿河岸上的分量大小与水流的速度大小相等,方向相反,有:v静•cosθ=v水 即为:cosθ=$\frac{3}{5}$得:θ=53°
即为:cosθ=$\frac{3}{5}$得:θ=53°
即为船头指向上游,与河岸间的夹角为53°
此时合速度为:v合=$\sqrt{{v}_{c}^{2}-{v}_{s}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4m/s
渡河时间为:t=$\frac{d}{{v}_{合}}$=$\frac{300}{4}$=75s
答:(1)要使船到达对岸的时间最短,船头应指向河对岸,最短时间为60s,在到达对岸偏下游350m位置.
(2)要使船航程最短,船头指向上游,与河岸间的夹角为53°,此时过河所用的时间为75s.
点评 该题通过渡河的模型考察了运动的合成与分解,关于渡河问题,应注意几种渡河方式,一是垂直渡河,此时渡河位移最短,但是所用时间不是最短的,此种情况要求船的合速度与河岸垂直,二是船头始终指向对岸的渡河,此种情况下渡河时间最短,但是渡河位移不是最短;关于渡河问题,还要会判断能否垂直渡河,其条件是船在静水中的速度大小要大于河水流动的速度大小.

 习题精选系列答案
习题精选系列答案| A. | 物体由于做圆周运动而产生一个向心力 | |
| B. | 向心力不改变匀速圆周运动物体的速度 | |
| C. | 匀速圆周运动的物体其向心力就是它所受的合外力 | |
| D. | 做匀速圆周运动物体其向心力是不变的 |
| A. | 做曲线运动的物体,其速度大小一定不断改变 | |
| B. | 做曲线运动的物体,其速度方向一定不断改变 | |
| C. | 做曲线运动的物体,其加速度大小一定不断改变 | |
| D. | 做曲线运动的物体,其加速度方向一定不断改变 |
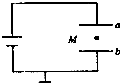 如图所示,两块水平放置的平行正对的金属板a、b与两电池相连,在距离两板等远的M点有一个带电液滴处于静止状态.若将b板向下平移一小段距离,稳定后,下列说法中正确的是( )
如图所示,两块水平放置的平行正对的金属板a、b与两电池相连,在距离两板等远的M点有一个带电液滴处于静止状态.若将b板向下平移一小段距离,稳定后,下列说法中正确的是( )| A. | 液滴将加速向下运动 | |
| B. | M点电势升高,液滴在M点时电势能将增大 | |
| C. | M点的电场强度变小了 | |
| D. | 在b板移动前后两种情况下,若将液滴从a板移到b板,电场力做功相同 |
| A. | i′=Imsinωt | B. | i′=4Imsin 2ωt | C. | i′=2Imsinωt | D. | i′=2Imsin 2ωt |
 如图所示,A、B两容器容积相等,用粗细均匀的细玻璃管相连,两容器内装有不同气体,细管中央有一段水银柱,在两边气体作用下保持平衡时,A中气体的温度为0℃,B中气体温度为20℃,如果将它们的温度都降低10℃,那么水银柱将( )
如图所示,A、B两容器容积相等,用粗细均匀的细玻璃管相连,两容器内装有不同气体,细管中央有一段水银柱,在两边气体作用下保持平衡时,A中气体的温度为0℃,B中气体温度为20℃,如果将它们的温度都降低10℃,那么水银柱将( )| A. | 向A移动 | B. | 向B移动 | C. | 不动 | D. | 不能确定 |
| A. | $\frac{F}{12}$ | B. | $\frac{4F}{3}$ | C. | 12F | D. | $\frac{3F}{4}$ |
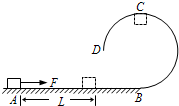 如图所示,粗糙水平轨道AB与固定在竖直面内的半径为R的四分之三粗糙圆轨道BCD在B点平滑连接.质量为m的物块(可视为质点)静止在A点.现用大小为F的水平恒力向右拉物块,使其沿水平轨道前进L后,突然撤去拉力F.物块到达圆轨道最高点C时,对轨道的压力大小恰好为零.重力加速度为g.求:
如图所示,粗糙水平轨道AB与固定在竖直面内的半径为R的四分之三粗糙圆轨道BCD在B点平滑连接.质量为m的物块(可视为质点)静止在A点.现用大小为F的水平恒力向右拉物块,使其沿水平轨道前进L后,突然撤去拉力F.物块到达圆轨道最高点C时,对轨道的压力大小恰好为零.重力加速度为g.求: