��Ŀ����
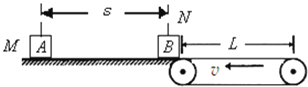
����Ŀ����ͼ��ˮƽ��MN�Ҷ�N����ˮƽ���ʹ�ǡ��ƽ���Һܿ��������ʹ�������v=lm/s��ʱ������ת����ˮƽ���ֳ���L=lm.���B��ֹ��ˮƽ������Ҷ�N��������ΪmA=lkg�����A�ھ�N��s=2.25m����v0=5m/s��ˮƽ���ٶ������˶�������B������ײ��ճ��һ����B��������A��k����A��B��ˮƽ��ʹ��ʹ��Ķ�Ħ��������Ϊ��=0.2����������Ϊ�ʵ㣬ȡg=l0m/s2.
��1����A����N����B��ײǰ���ٶȴ�С��
��2������ײ��˲��AB���ٶȴ�С����ײ�����в��������ܣ�
��3������k�ڲ�ͬ��ֵ��Χʱ��A��B��ײ���ʹ������������Ĺ�W�ı���ʽ
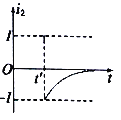
���𰸡���1��4m/s��2��![]() ��
�� ![]() ��3����������
��3����������
����������1������ײǰA���ٶ�Ϊv1.�ɶ��ܶ�����![]() ����ã�
����ã� ![]()
��2������ײ��A��B�ٶ�Ϊv2����������Ϊ�������ɶ����غ㶨�ɵ�![]() ����ã�
����ã� ![]()
��ϵͳ����ת�����غ�ɵ�![]() ����ã�
����ã� ![]()
��3�������AB�ܴӴ��ʹ��Ҳ��뿪������������ ![]() ����ã�
����ã� ![]()
���ʹ������������Ĺ�![]()
����v2��vʱ�У�k��3
��AB�ȼ��ٵ�0�ٷ��أ������ʹ����ʱ�ٶ���Ϊv2��
������̴��ʹ���AB�����Ĺ�![]()
����1��k<3ʱ��AB�ش��ʹ����Ҽ��ٵ��ٶ�Ϊ�㣬��������٣����ٶ��봫�ʹ��ٶ����ʱ�봫�ʹ�һ�������˶������ʹ�����ˡ�
����������д��ʹ���AB�����Ĺ�![]() ����ã�
����ã� ![]()