题目内容
4.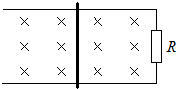 如图所示间距为L的光滑平行金属导轨,水平放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻为R0、质量为m的导体棒放置在导轨上,在外力作用下从t=0的时刻开始运动,其速度随时间的变化规律v=vmsinωt,不计导轨电阻.则从t=0到t=$\frac{π}{2ω}$时间内外力F所做的功为( )
如图所示间距为L的光滑平行金属导轨,水平放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻为R0、质量为m的导体棒放置在导轨上,在外力作用下从t=0的时刻开始运动,其速度随时间的变化规律v=vmsinωt,不计导轨电阻.则从t=0到t=$\frac{π}{2ω}$时间内外力F所做的功为( )| A. | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω(R+{R_0})}}$+$\frac{1}{2}$mvm2 | B. | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω(R+{R_0})}}$ | ||
| C. | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω(R+{R_0})}}$-$\frac{1}{2}$mvm2 | D. | $\frac{{π{B^2}{L^2}v_m^2}}{{2ω(R+{R_0})}}$ |
分析 根据感应电动势和电路公式,并由动能定理研究从t=0到t=$\frac{π}{2ω}$ 时间内,其中克服安培力做功大小等于电路中产生的热量,从而即可求解.
解答 解:根据感应电动势和电路得:
E=BLv=I(R+R0)
则有:I=$\frac{BLV}{R+{R}_{0}}$
根据动能定理研究从t=0到t=$\frac{π}{2ω}$ 时间内
WF+W安=$\frac{1}{2}$mvm2-0
安培力做功量度电能变化的多少,根据v=vmsinωt,知道电路中产生的电流为正弦交变电流,
∴W安=-Q=-$\frac{{B}^{2}{L}^{2}{V}_{m}^{2}}{2(R+{R}_{0})}$•t=$\frac{π{B}^{2}{L}^{2}{{V}_{m}}^{2}}{4ω(R+{R}_{0})}$,
WF=$\frac{1}{2}$mvm2+$\frac{π{B}^{2}{L}^{2}{{V}_{m}}^{2}}{4ω(R+{R}_{0})}$,故A正确,BCD错误.
故选:A.
点评 能够把电磁感应和动能定理结合解决问题.知道正弦交变电流产生热量的求解方式.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
3.关于质点做匀速圆运动的下列说法中正确的是( )
| A. | 由a=$\frac{{v}^{2}}{r}$知a与r成反比 | B. | 由a=ω2r知a与r成正比 | ||
| C. | 由ω=$\frac{v}{r}$知,ω与r成反比 | D. | 由ω=2пn知ω与n成正比(n为转速) |
12.一汽车通过拱形桥顶时恰对桥面没有压力,这时汽车的速度为10m/s,则拱形桥的半径为( )(g取10m/s2)
| A. | 1m | B. | 10m | C. | 10m | D. | 20m |
19.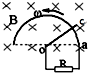 如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )
如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )
 如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )
如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )| A. | $\frac{{B}^{2}{r}^{2}{ω}^{4}}{4R}$ | B. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{4R}$ | C. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{2R}$ | D. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{9R}$ |
16.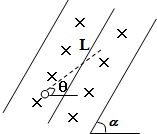 实线表示竖直平面内匀强电场的电场线,电场线与水平方面成α角,匀强磁场与电场正交,垂直纸面向里.有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成θ角,且α>θ,则下列说法中正确的是( )
实线表示竖直平面内匀强电场的电场线,电场线与水平方面成α角,匀强磁场与电场正交,垂直纸面向里.有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成θ角,且α>θ,则下列说法中正确的是( )
 实线表示竖直平面内匀强电场的电场线,电场线与水平方面成α角,匀强磁场与电场正交,垂直纸面向里.有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成θ角,且α>θ,则下列说法中正确的是( )
实线表示竖直平面内匀强电场的电场线,电场线与水平方面成α角,匀强磁场与电场正交,垂直纸面向里.有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成θ角,且α>θ,则下列说法中正确的是( )| A. | 液滴一定做匀变速直线运动 | B. | 液滴一定带正电 | ||
| C. | 电场线的方向一定斜向上 | D. | 液滴有可能做匀速直线运动 |
13. 如图,是霍尔元件的原理示意图,如果用d表示薄片的厚度,k为霍尔系数,对于一个霍尔元件d、k为定值,如果保持电流I恒定,则可以验证UH随B的变化情况.下列说法错误的是( )
如图,是霍尔元件的原理示意图,如果用d表示薄片的厚度,k为霍尔系数,对于一个霍尔元件d、k为定值,如果保持电流I恒定,则可以验证UH随B的变化情况.下列说法错误的是( )
 如图,是霍尔元件的原理示意图,如果用d表示薄片的厚度,k为霍尔系数,对于一个霍尔元件d、k为定值,如果保持电流I恒定,则可以验证UH随B的变化情况.下列说法错误的是( )
如图,是霍尔元件的原理示意图,如果用d表示薄片的厚度,k为霍尔系数,对于一个霍尔元件d、k为定值,如果保持电流I恒定,则可以验证UH随B的变化情况.下列说法错误的是( )| A. | 霍尔元件是一种磁传感器,即对磁场有敏感的反应 | |
| B. | 将永磁体的一个磁极逐渐靠近霍尔元件的工作面时,UH将变大 | |
| C. | 在测定地球赤道上的磁场强弱时,霍尔元件的工作面应保持水平 | |
| D. | 改变磁感线与霍尔元件工作面的夹角时UH将会发生变化 |
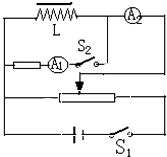 某同学利用如图所示的电路,测定一个自感系数很大的线圈L的直流电阻RL,实验室提供下列器材:
某同学利用如图所示的电路,测定一个自感系数很大的线圈L的直流电阻RL,实验室提供下列器材:
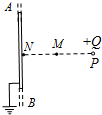 如图所示,AB是一个接地的很大的薄金属板,其右侧P点有一带电量为Q的正点电荷,N为金属板右侧表面上的一点,P到金属板的垂直距离PN=d,M为PN连线的中点.关于M,N两点的场强和电势,有如下说法:
如图所示,AB是一个接地的很大的薄金属板,其右侧P点有一带电量为Q的正点电荷,N为金属板右侧表面上的一点,P到金属板的垂直距离PN=d,M为PN连线的中点.关于M,N两点的场强和电势,有如下说法: