题目内容
9.如图所示,一个带$\frac{1}{4}$圆弧轨道的平台固定在水平地面上,光滑圆弧MN的半径为R=3.2m,水平部分NP长L=3.5m,物体B静止在足够长的平板小车C上,B与小车的接触面光滑,小车的左端紧贴平台的右端.从M点由静止释放的物体A滑至轨道最右端P点后再滑上小车,物体A滑上小车后若与物体B相碰必粘在一起,它们间无竖直作用力.A与平台水平轨道和小车上表面的动摩擦因数都为0.4,且最大静摩擦力与滑动摩擦力大小相等.物体A、B和小车C的质量均为1kg,取g=10m/s2.求:
(1)物体A进入N点前瞬间对轨道的压力大小?
(2)物体A在NP上运动的时间?
(3)物体A最终离小车左端的距离为多少?
分析 (1)由动能定理求出A到达N点的速度,然后由牛顿第二定律求物体A进入N点所受的支持力,进而由牛顿第三定律求物体对轨道N的压力;
(2)由牛顿第二定律和位移时间公式求物体在NP上运动的时间;
(3)小车、物体A、B组成系统满足动量守恒,然后结合动能定理和运动学公式列方程联立求解.
解答 解:(1)物体A由M到N过程中,由动能定理得:
mAgR=$\frac{1}{2}$mAvN2
在N点,由牛顿定律得
FN-mAg=mA$\frac{{v}_{N}^{2}}{R}$
由①、②得FN=3mAg=30N
由牛顿第三定律得,物体A进入轨道前瞬间对轨道压力大小为:FN′=3mAg=30N
(2)物体A在平台上运动过程中
μmAg=mAa
L=vNt-$\frac{1}{2}$at2
由①、⑤、⑥式得 t=0.5s t=3.5s(不合题意,舍去)
(3)物体A刚滑上小车时速度 v1=vN-at=6m/s
从物体A滑上小车到相对小车静止过程中,小车、物体A组成系统动量守恒,而物体B保持静止
(m A+mC)v2=mAv1
小车最终速度 v2=3m/s
此过程中A相对小车的位移为L1,则$μmg{L_1}=\frac{1}{2}m{v_1}^2-\frac{1}{2}×2m{v_2}^2$解得:L1=$\frac{9}{4}m$
物体A与小车匀速运动直到A碰到物体B,A,B相互作用的过程中动量守恒:
(m A+mB)v3=mAv2
此后A,B组成的系统与小车发生相互作用,动量守恒,且达到共同速度v4
(m A+mB)v3+mCv2=(mA+mB+mC) v4
此过程中A相对小车的位移大小为L2,则$μmg{L_2}=\frac{1}{2}m{v_2}^2+\frac{1}{2}×2m{v_3}^2-\frac{1}{2}×3m{v_4}^2$
解得:L2=$\frac{3}{16}m$
物体A最终离小车左端的距离为x=L1-L2=$\frac{33}{16}m$
答:(1)物体A进入N点前瞬间对轨道的压力大小为30N;
(2)物体A在NP上运动的时间为0.5s;
(3)物体A最终离小车左端的距离为$\frac{33}{16}m$
点评 本题综合运用了牛顿第二定律、动能定理、运动学公式、动量守恒定律,综合性较强,要求能正确分析题意,明确物理过程做好受力分析,然后再选择合适的物理规律求解即可.

 阅读快车系列答案
阅读快车系列答案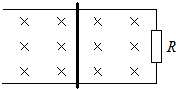 如图所示间距为L的光滑平行金属导轨,水平放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻为R0、质量为m的导体棒放置在导轨上,在外力作用下从t=0的时刻开始运动,其速度随时间的变化规律v=vmsinωt,不计导轨电阻.则从t=0到t=$\frac{π}{2ω}$时间内外力F所做的功为( )
如图所示间距为L的光滑平行金属导轨,水平放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻为R0、质量为m的导体棒放置在导轨上,在外力作用下从t=0的时刻开始运动,其速度随时间的变化规律v=vmsinωt,不计导轨电阻.则从t=0到t=$\frac{π}{2ω}$时间内外力F所做的功为( )| A. | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω(R+{R_0})}}$+$\frac{1}{2}$mvm2 | B. | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω(R+{R_0})}}$ | ||
| C. | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω(R+{R_0})}}$-$\frac{1}{2}$mvm2 | D. | $\frac{{π{B^2}{L^2}v_m^2}}{{2ω(R+{R_0})}}$ |
| A. | $\frac{2L}{g{t}^{2}cosα}$-tanα,t$\sqrt{\frac{L}{g{t}^{2}sinα-L}}$ | B. | $\frac{Lcosα}{g{t}^{2}}$-tanα,t$\sqrt{\frac{gL}{{t}^{2}sinα-L}}$ | ||
| C. | $\frac{Lsinα}{{t}^{2}}$-cosα,t$\sqrt{\frac{gL}{{t}^{2}cosα-L}}$ | D. | $\frac{Ltanα}{g{t}^{2}}$-cosα,t$\sqrt{\frac{2gL}{g{t}^{2}-L}}$ |
 如图所示,密闭容器内的氢气温度与外界空气的温度相同,现对该容器缓慢加热,当容器内的氢气温度高于外界空气的温度时,则( )
如图所示,密闭容器内的氢气温度与外界空气的温度相同,现对该容器缓慢加热,当容器内的氢气温度高于外界空气的温度时,则( )| A. | 氢分子的平均动能增大 | B. | 氢分子的势能增大 | ||
| C. | 容器内氢气的内能增大 | D. | 容器内氢气的内能可能不变 | ||
| E. | 容器内氢气的压强增大 |
| A. | 牛顿总结出了万有引力定律并测出了引力常量,被后人称为称出地球的第一人 | |
| B. | 伽利略总结出太阳系行星运动的三大规律 | |
| C. | 亚里士多德通过理想实验提出力并不是维持物体运动的原因 | |
| D. | 胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 |
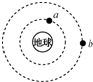
| A. | a卫星的运行速度比第一宇宙速度大 | |
| B. | b卫星的运行速度比a卫星的小 | |
| C. | b卫星的周期比a卫星的小 | |
| D. | b卫星的角速度比a卫星的大 |
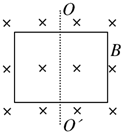 如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直,则穿过平面的磁通量为BS.若使框架绕OO′转过60°角,则穿过框架平面的磁通量为$\frac{1}{2}$BS.
如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直,则穿过平面的磁通量为BS.若使框架绕OO′转过60°角,则穿过框架平面的磁通量为$\frac{1}{2}$BS.