Question

一物块从倾角为θ、长为s的斜面的顶端由静止开始下滑，物块与斜面间的动摩擦因数为μ，求物块滑到斜面底端所需的时间．

Answer 1

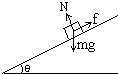解：设物块质量为m，加速度为a，物块受力情况如图所示，
mgsinθ-f=ma，
N-mgcosθ=0，
f=μN，
联立三式解得 a=gsinθ-μgcosθ
由　　s=
．
分析：根据牛顿第二定律求出物块下滑的加速度a，再根据匀变速直线运动的位移时间公式s=求出物块滑到斜面底端所需的时间．
点评：解决本题的关键知道加速度是联系运动学和力学的桥梁，根据受力求出加速度，根据运动学公式求出时间．