题目内容
15. 某一空间存在着磁感应强度为B且大小恒定、方向随时间t做周期性变化的匀强磁场(如图甲所示),磁场变化的周期为T,规定垂直纸面向里的磁场方向为正.一个带正电的粒子从a点开始只在磁场力的作用恰能按a→b→c→d→e→f的顺序做横“∞”字曲线运动(即如图乙所示的轨迹,两圆的半径可为任意值),则( )
某一空间存在着磁感应强度为B且大小恒定、方向随时间t做周期性变化的匀强磁场(如图甲所示),磁场变化的周期为T,规定垂直纸面向里的磁场方向为正.一个带正电的粒子从a点开始只在磁场力的作用恰能按a→b→c→d→e→f的顺序做横“∞”字曲线运动(即如图乙所示的轨迹,两圆的半径可为任意值),则( )| A. | 在t=$\frac{T}{4}$时给粒子一个沿切线方向水平向右的初速度可以实现该运动轨迹 | |
| B. | 在t=$\frac{3T}{8}$时给粒子一个沿切线方向水平向右的初速度可以实现该运动轨迹 | |
| C. | 在t=$\frac{5T}{8}$时给粒子一个沿切线方向水平向左的初速度可以实现该运动轨迹 | |
| D. | 该粒子的比荷$\frac{q}{m}$=$\frac{4π}{BT}$ |
分析 带电粒子在磁场中运动时受到洛伦兹力而偏转,根据左手定则判断洛伦兹力方向,结合时间与周期的关系分析粒子的运动轨迹.
解答  解:A、粒子初始位置在a处,t=$\frac{T}{4}$T时给粒子一个沿切线方向水平向右的初速度,此时磁场方向垂直纸面向里,根据左手定则判断可知,洛伦兹力向上,沿逆时针方向从a运动到b,$\frac{T}{4}$时间后磁场方向变为垂直纸面向外,洛伦兹力方向向右,经过$\frac{T}{2}$时间内,即t=T时刻粒子沿bc圆周运动半周到达g点,t=T起磁场方向向里,洛伦兹力方向向右,粒子将离开磁场,不可能到达f,不符合题意,故A错误.
解:A、粒子初始位置在a处,t=$\frac{T}{4}$T时给粒子一个沿切线方向水平向右的初速度,此时磁场方向垂直纸面向里,根据左手定则判断可知,洛伦兹力向上,沿逆时针方向从a运动到b,$\frac{T}{4}$时间后磁场方向变为垂直纸面向外,洛伦兹力方向向右,经过$\frac{T}{2}$时间内,即t=T时刻粒子沿bc圆周运动半周到达g点,t=T起磁场方向向里,洛伦兹力方向向右,粒子将离开磁场,不可能到达f,不符合题意,故A错误.
B、粒子初始位置在a处,t=$\frac{3}{8}$T时给粒子一个沿切线方向水平向右的初速度,此时磁场方向垂直纸面向里,根据左手定则判断可知,洛伦兹力向上,沿逆时针方向从a运动到b,$\frac{T}{8}$时间后磁场方向变为垂直纸面向外,洛伦兹力方向向右,经过$\frac{T}{2}$沿bcd圆周运动一周回到b,此时磁场方向向里,粒子沿bcf圆弧运动$\frac{3T}{8}$时间,恰好回到a点,接着周而复始,故粒子能做横“∞”字曲线运动且逆时针方向通过efab.故B正确.
C、在t=$\frac{5T}{8}$时给粒子一个沿切线方向水平向左,此时磁场方向垂直纸面向外,根据左手定则判断可知,洛伦兹力向上,沿顺时针方向从a运动到f,不符合题意,故C错误.
D、由B项分析可知,粒子在磁场中运动的周期必须为 T′=$\frac{T}{2}$,由T′=$\frac{2πm}{qB}$,则得该粒子的比荷$\frac{q}{m}$=$\frac{4π}{BT}$.故D正确.
故选:BD.
点评 本题关键运用左手定则分析带电粒子所的洛伦兹力方向,从而判断其运动情况.本题解题思路简单清晰,当过程复杂,分析起来比较麻烦,解题时要细心、认真,否则会出错.

 极光是由来自太阳的高能量带电粒子流高速冲进高空稀薄大气层时,被地球磁场俘获,从而改变原有运动方向,向两极做螺旋运动,科学家发现并证实,向两极做螺旋运动的这些高能粒子的旋转半径是不断减小的,这主要与下列哪些因素有关( )
极光是由来自太阳的高能量带电粒子流高速冲进高空稀薄大气层时,被地球磁场俘获,从而改变原有运动方向,向两极做螺旋运动,科学家发现并证实,向两极做螺旋运动的这些高能粒子的旋转半径是不断减小的,这主要与下列哪些因素有关( )| A. | 洛伦兹力对粒子做负功,使其动能减小 | |
| B. | 空气阻力做正功,使其动能减小 | |
| C. | 靠近南北两极的磁感应强度增强 | |
| D. | 太阳对粒子的引力做负功 |
 如图所示,上部半圆下部矩形组成的平面区域内存在垂直平面向里的匀强磁场,由点A向圆心O方向连续发射相同速率的同种带电粒子,最终粒子从B点离开磁场区域,不计粒子所受重力,粒子间的相互作用及空气阻力,则以下说法正确的是( )
如图所示,上部半圆下部矩形组成的平面区域内存在垂直平面向里的匀强磁场,由点A向圆心O方向连续发射相同速率的同种带电粒子,最终粒子从B点离开磁场区域,不计粒子所受重力,粒子间的相互作用及空气阻力,则以下说法正确的是( )| A. | 该种粒子一定带负电,且在B点沿OB方向离开磁场 | |
| B. | 若在A点增大粒子入射速率,方向不变,则粒子在磁场中的运动时间增加 | |
| C. | 若在A点调整粒子入射方向,速率不变,则BC间无粒子射出 | |
| D. | 若在A点调整粒子入射方向,速率不变,从AB弧射出的粒子的出射方向均与OB平行 |
 如图,质量为m的均匀半圆形薄板,可以绕光滑水平轴A在竖直平面内转动,AB是它的直径,O是圆心.在B点作用一个竖直向上的力F使薄板平衡,此时AB恰处于水平位置,若保持力F始终竖直向上,在F作用下使薄板绕A点沿逆时针方向缓慢转动,直到AB接近竖直位置的过程中,力F对应的力矩为M,则M、F大小变化情况是( )
如图,质量为m的均匀半圆形薄板,可以绕光滑水平轴A在竖直平面内转动,AB是它的直径,O是圆心.在B点作用一个竖直向上的力F使薄板平衡,此时AB恰处于水平位置,若保持力F始终竖直向上,在F作用下使薄板绕A点沿逆时针方向缓慢转动,直到AB接近竖直位置的过程中,力F对应的力矩为M,则M、F大小变化情况是( )| A. | M变小,F不变 | B. | M、F均变大 | ||
| C. | M、F均先变大再变小 | D. | M先变大再变小,F始终变大 |
 如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )
如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )| A. | 在乙图中将做往复运动 | |
| B. | 在甲图中将做匀加速直线运动 | |
| C. | 在乙图中向O2点运动时,加速度一定减小 | |
| D. | 在乙图中到达O2点时动能最小,电势能最大 |
| A. | 为实现对接,两者运行速度的大小都应介于第一宇宙速度和第二宇宙速度之间 | |
| B. | 如不加干预,在运行一段时间后,天宫一号的动能可能会减小 | |
| C. | 如不加干预,天宫一号的轨道高度将缓慢降低 | |
| D. | 航天员在天宫一号中处于失重状态,说明航天员不受地球引力作用 |


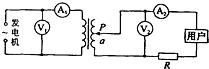 如图所示,理想变压器原线圈匝数 n1=140匝,副线圈总匝数 n2=1400匝,原线圈电压μ1=10V,线路电阻用R表示,R=4,用户电阻R′=16Ω.开始时滑动触头P放在副线圈的中点,不计电表对电路的影响,求:
如图所示,理想变压器原线圈匝数 n1=140匝,副线圈总匝数 n2=1400匝,原线圈电压μ1=10V,线路电阻用R表示,R=4,用户电阻R′=16Ω.开始时滑动触头P放在副线圈的中点,不计电表对电路的影响,求: