题目内容
19. 如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )| A. | 运动周期相同 | B. | 运动线速度一样 | ||
| C. | 运动向心加速度相同 | D. | 细线所受拉力大小相同 |
分析 两个小球均做匀速圆周运动,对它们受力分析,找出向心力来源,可先求出角速度,再由角速度与线速度、周期、向心加速度的关系公式求解.
解答 解:A、对其中一个小球受力分析,如图,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;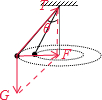
将重力与拉力合成,合力指向圆心,由几何关系得,合力:F=mgtanθ…①;
由向心力公式得到:F=mω2r…②;
设绳子与悬挂点间的高度差为h,由几何关系,得:r=htanθ…③;
由①②③三式得:ω=$\sqrt{\frac{g}{h}}$,与绳子的长度和转动半径无关,又由T=$\frac{2π}{ω}$知,周期相同,故A正确;
B、由v=ωr,两球转动半径不等,故B错误;
C、由a=ω2r,两球转动半径不等,故C错误;
D、细线的拉力 T=$\frac{mg}{cosθ}$,因θ不同,故T不同,故D错误;
故选:A.
点评 本题关键要对球受力分析,确定向心力来源,求角速度;同时要灵活应用角速度与线速度、向心加速度之间的关系公式.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
9.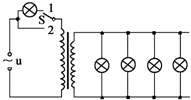 有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )
有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )
 有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )
有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )| A. | 该变压器是降压变压器,原、副线圈匝数比为4:1 | |
| B. | 该变压器是升压变压器,原、副线圈匝数比为1:4 | |
| C. | 副线圈中的灯泡仍能发光,只是更亮些 | |
| D. | 副线圈中的灯泡仍能发光,只是亮度变暗 |
10.有两颗地球同步卫星,下列关于它们的说法正确的是( )
| A. | 轨道半径可以不同 | |
| B. | 线速度大小可以不同 | |
| C. | 均有可能通过滕州上空 | |
| D. | 运行的线速度一定小于第一宇宙速度 |
14.关于平抛物体的运动,下列说法中正确的是( )
| A. | 平抛物体做的是瞬时速度时刻变化、加速度恒定不变的匀变速曲线运动 | |
| B. | 初速度越大,物体在空中运动的时间越长 | |
| C. | 物体落地时的水平位移与初速度无关 | |
| D. | 物体在任意相等时间内的速度变化量大小相等,方向不同 |
4.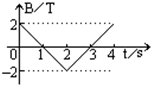 一个面积S=4×10-2m2、匝数N=102匝的线圈,放在匀强磁场中,磁场方向垂直线圈平面,磁场的磁感应强度B随时间t的变化规律如图所示.则( )
一个面积S=4×10-2m2、匝数N=102匝的线圈,放在匀强磁场中,磁场方向垂直线圈平面,磁场的磁感应强度B随时间t的变化规律如图所示.则( )
 一个面积S=4×10-2m2、匝数N=102匝的线圈,放在匀强磁场中,磁场方向垂直线圈平面,磁场的磁感应强度B随时间t的变化规律如图所示.则( )
一个面积S=4×10-2m2、匝数N=102匝的线圈,放在匀强磁场中,磁场方向垂直线圈平面,磁场的磁感应强度B随时间t的变化规律如图所示.则( )| A. | 在开始2s内穿过线圈磁通量的变化率等于8wb/s | |
| B. | 在开始2s内穿过线圈磁通量的变化量等于零 | |
| C. | 在开始2s内线圈中产生的感应电动势等于8V | |
| D. | 在第3s末线圈中产生的感应电动势为零 |
11.今将同一根条形磁铁缓慢地或迅速地全部插入一闭合线圈中,试比较在上述两过程中,相同的物理量是( )
| A. | 磁通量的变化量 | B. | 外力所做的功 | ||
| C. | 感应电动势的平均值 | D. | 通过线圈导线横截面的电量 |
16.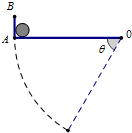 如图OA为可以绕O点转动的光滑挡板,AB为垂直于OA的光滑挡板.OA开始时处于水平状态,有一小球静止与AB和OA的连接处.现让挡板OA绕O点逆时针缓慢转过θ=60°,该过程中OA和AB对小球的作用力N1和N2的大小变化情况为( )
如图OA为可以绕O点转动的光滑挡板,AB为垂直于OA的光滑挡板.OA开始时处于水平状态,有一小球静止与AB和OA的连接处.现让挡板OA绕O点逆时针缓慢转过θ=60°,该过程中OA和AB对小球的作用力N1和N2的大小变化情况为( )
 如图OA为可以绕O点转动的光滑挡板,AB为垂直于OA的光滑挡板.OA开始时处于水平状态,有一小球静止与AB和OA的连接处.现让挡板OA绕O点逆时针缓慢转过θ=60°,该过程中OA和AB对小球的作用力N1和N2的大小变化情况为( )
如图OA为可以绕O点转动的光滑挡板,AB为垂直于OA的光滑挡板.OA开始时处于水平状态,有一小球静止与AB和OA的连接处.现让挡板OA绕O点逆时针缓慢转过θ=60°,该过程中OA和AB对小球的作用力N1和N2的大小变化情况为( )| A. | N1和N2均一直增大 | B. | N1和N2均一直减小 | ||
| C. | N1一直减小、N2一直增大 | D. | N1先减小后增大、N2一直增大 |
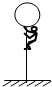 如图所示,载人气球原悬浮于离地高度为h的空中,气球质量为M,人的质量为m.若人要沿绳梯着地,则绳梯长至少是$\frac{M+m}{M}h$.
如图所示,载人气球原悬浮于离地高度为h的空中,气球质量为M,人的质量为m.若人要沿绳梯着地,则绳梯长至少是$\frac{M+m}{M}h$.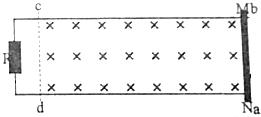 如图所示,固定于绝缘水平面上且间距d=0.2m的U形金属框架处在竖直向下、均匀分布的磁场中,磁场的左边界cd与右边界ab之间的距离L=1m,t=0时,长为d的金属棒MN从ab处开始沿框架以初速度v0=0.2m/s向左运动,5s时棒刚好到达cd处停下;t=0时刻开始,磁场的磁感应强度B从B0=0.2T开始随时间t变化而正好使得第1s内导体棒可以做匀速运动,在接下来的时间内B保持不变,其中R=0.4Ω,棒的电阻r=0.1Ω,不计其他电阻和一切摩擦阻力,棒与导轨始终垂直且接触良好,求:
如图所示,固定于绝缘水平面上且间距d=0.2m的U形金属框架处在竖直向下、均匀分布的磁场中,磁场的左边界cd与右边界ab之间的距离L=1m,t=0时,长为d的金属棒MN从ab处开始沿框架以初速度v0=0.2m/s向左运动,5s时棒刚好到达cd处停下;t=0时刻开始,磁场的磁感应强度B从B0=0.2T开始随时间t变化而正好使得第1s内导体棒可以做匀速运动,在接下来的时间内B保持不变,其中R=0.4Ω,棒的电阻r=0.1Ω,不计其他电阻和一切摩擦阻力,棒与导轨始终垂直且接触良好,求: