题目内容
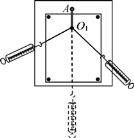
【题目】如图所示,一质量M=4kg的小车静置于光滑水平地面上,左侧用固定在地面上的销钉挡住。小车上表面由光滑圆弧轨道BC和水平粗糙轨道CD组成,BC与CD相切于C, BC所对圆心角θ=37°,CD长L=3m。质量m=1kg的小物块从某一高度处的A点以v0=4m/s的速度水平抛出,恰好沿切线方向自B点进入圆弧轨道,滑到D点时刚好与小车达到共同速度v=1.2m/s。取g=10m/s2,sin37°=0.6,忽略空气阻力。
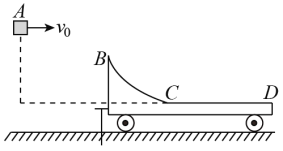
(1)求A、B间的水平距离x;
(2)求小物块从C滑到D所用时间t0;
(3)求圆弧半径R.
【答案】(1) x=1.2m (2) t0=1s (3) 2.75m
【解析】
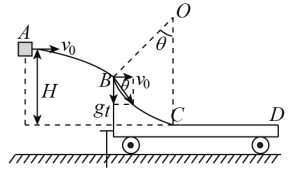
(1)由平抛运动的规律得
tanθ=![]() x= v0t
x= v0t
得x=1.2m
(2)物块在小车上CD段滑动过程中,由动量守恒定律得 mv1=(M+m) v
解得v1=6m/s
由功能关系得 fL=![]() mv12-
mv12-![]() (M+m)v2
(M+m)v2
对物块,由动量定理得 -ft0=mv-mv1
得t0=1s
(3) 物块进入B点时的速度![]() ,到达C点的速度为vC=v1=6m/s,
,到达C点的速度为vC=v1=6m/s,
滑块从B到C的机械能守恒,由机械能守恒定律得:![]()
解得:R=2.75m

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目