题目内容
 如图所示,已知O、A、B、C为同一直线上的四点,OA间的距离为l1,BC间的距离为l2,一物体自O点静止起出发,沿此直线做匀加速运动,依次经过A、B、C三点.已知物体通过OA段与通过BC段所用时间相等.求O与C的距离.
如图所示,已知O、A、B、C为同一直线上的四点,OA间的距离为l1,BC间的距离为l2,一物体自O点静止起出发,沿此直线做匀加速运动,依次经过A、B、C三点.已知物体通过OA段与通过BC段所用时间相等.求O与C的距离.分析:设物体的加速度为a,到达B点的速度为vB,根据运动学位移公式分别研究OA段和BC段,联立求出vB,再公式v2-
=2as,求出AB距离,即求解O与C的距离.
| v | 2 0 |
解答:解:设物体的加速度为a,到达B点的速度为vB,通过OA段和BC段所用的时间为t,则有:
l1=
at2 …①
l2=vBt+=
at2…②
联立①②式得:vB=
…③
设O与B的距离为SOB,则有:SOB=
…④
联立①③④式得:SOB=
…⑤
所以OC间的距离为SOC=SOB+l2=
…⑥
答:O与C的距离是
.
l1=
| 1 |
| 2 |
l2=vBt+=
| 1 |
| 2 |
联立①②式得:vB=
| l2-l1 |
| t |
设O与B的距离为SOB,则有:SOB=
| ||
| 2a |
联立①③④式得:SOB=
| (l2-l1)2 |
| 4l1 |
所以OC间的距离为SOC=SOB+l2=
| (l1+l2)2 |
| 4l1 |
答:O与C的距离是
| (l1+l2)2 |
| 4l1 |
点评:本题运用运动学的基本公式研究时,关键要灵活选择研究的过程,也可以运用推论△s=aT2,得到加速度的表达式,再与其他公式结合求解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图所示,已知带电小球A、B的电荷量分别为QA、QB,OA=OB,都用长L的绝缘丝线悬挂在绝缘墙角O点处.静止时A、B相距为d.为使平衡时AB间距离减为d/2,可采用以下哪些方法( )
如图所示,已知带电小球A、B的电荷量分别为QA、QB,OA=OB,都用长L的绝缘丝线悬挂在绝缘墙角O点处.静止时A、B相距为d.为使平衡时AB间距离减为d/2,可采用以下哪些方法( )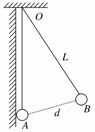
 如图所示,已知O、A、B、C为同一直线上的四点,OA间的距离为l1,BC间的距离为l2,一物体自O点静止起出发,沿此直线做匀加速运动,依次经过A、B、C三点.已知物体通过OA段与通过BC段所用时间相等.求O与C的距离.
如图所示,已知O、A、B、C为同一直线上的四点,OA间的距离为l1,BC间的距离为l2,一物体自O点静止起出发,沿此直线做匀加速运动,依次经过A、B、C三点.已知物体通过OA段与通过BC段所用时间相等.求O与C的距离.