题目内容
7.如图所示,两条平行光滑导轨相距L,左端一段被弯成半径为H的$\frac{1}{4}$圆弧,圆弧导轨所在区域无磁场.水平导轨区域存在着竖直向上的匀强磁场B,右端连接阻值为R的定值电阻,水平导轨足够长.在圆弧导轨顶端放置一根质量为m的金属棒ab,导轨好金属棒ab的电阻不计,重力加速度为g,现让金属棒由静止开始运动,整个运动过程金属棒和导轨接触紧密.求:(1)金属棒进入水平导轨时,通过金属棒的感应电流的大小和方向.
(2)整个过程中电阻R产生的焦耳热.
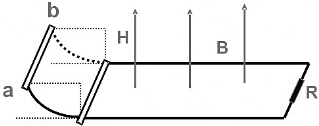
分析 (1)ab棒沿圆弧轨道下滑的过程遵守机械能守恒,由机械能守恒定律求出它到达圆弧最低端时的速度,由右手定则判断感应电流的方向,由E=BLv和欧姆定律结合求感应电流的大小.
(2)金属棒ab进入水平轨道后受到安培阻力而作减速运动,最终静止,由能量守恒定律求整个过程中电阻R产生的焦耳热.
解答 解:(1)ab棒沿圆弧轨道下滑的过程,只有重力做功,由机械能守恒定律得
mgH=$\frac{1}{2}m{v}^{2}$
可得 v=$\sqrt{2gH}$
金属棒进入水平导轨时产生的感应电动势为 E=BLv
通过金属棒的感应电流为 I=$\frac{E}{R}$
联立得 I=$\frac{BL\sqrt{2gH}}{R}$
由右手定则判断知,通过金属棒的感应电流的方向由b→a.
(2)由能量守恒定律可知,整个过程中电阻R产生的焦耳热 Q=mgH
答:
(1)金属棒进入水平导轨时,通过金属棒的感应电流的大小为$\frac{BL\sqrt{2gH}}{R}$,方向由b→a.
(2)整个过程中电阻R产生的焦耳热为mgH.
点评 本题是电磁感应与电路的综合,关键要掌握电磁感应的基本规律,如法拉第电磁感应定律、欧姆定律和右手定则,并能熟练运用.

练习册系列答案
相关题目
19.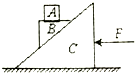 如图所示,物体B的上表面水平,C受到向左的水平推力F时,A、B、C静止,下列说法正确的是( )
如图所示,物体B的上表面水平,C受到向左的水平推力F时,A、B、C静止,下列说法正确的是( )
 如图所示,物体B的上表面水平,C受到向左的水平推力F时,A、B、C静止,下列说法正确的是( )
如图所示,物体B的上表面水平,C受到向左的水平推力F时,A、B、C静止,下列说法正确的是( )| A. | 物体A受到3个力作用 | B. | 物体B受到4个力作用 | ||
| C. | 物体C受到5个力作用 | D. | 物体C对地面的压力等于C的重力 |
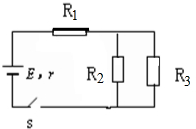
2.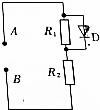 如图所示,电路中的电阻R1与电阻R2的阻值均为R,和R1并联的D为理想二极管(正向电阻可看作零,反向电阻可看作无穷大).在A、B间加某A一正弦交流电压时.则加在R2上的电压有效值为5$\sqrt{10}$V,由此可知这一正弦交流电压的最大值为( )
如图所示,电路中的电阻R1与电阻R2的阻值均为R,和R1并联的D为理想二极管(正向电阻可看作零,反向电阻可看作无穷大).在A、B间加某A一正弦交流电压时.则加在R2上的电压有效值为5$\sqrt{10}$V,由此可知这一正弦交流电压的最大值为( )
 如图所示,电路中的电阻R1与电阻R2的阻值均为R,和R1并联的D为理想二极管(正向电阻可看作零,反向电阻可看作无穷大).在A、B间加某A一正弦交流电压时.则加在R2上的电压有效值为5$\sqrt{10}$V,由此可知这一正弦交流电压的最大值为( )
如图所示,电路中的电阻R1与电阻R2的阻值均为R,和R1并联的D为理想二极管(正向电阻可看作零,反向电阻可看作无穷大).在A、B间加某A一正弦交流电压时.则加在R2上的电压有效值为5$\sqrt{10}$V,由此可知这一正弦交流电压的最大值为( )| A. | 10V | B. | 10$\sqrt{2}$V | C. | 20V | D. | 20$\sqrt{2}$V |
12.如图所示灯,灯泡a、b、c完全相同.线圈L稳流电阻不计且自感系数足够大.则下列判断正确的有( )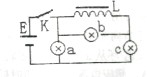

| A. | K闭合的瞬间,b、c两灯几乎一样亮 | |
| B. | K闭合稳定后,a、c两灯一样亮 | |
| C. | K断开之后的短时间内,b灯中有向左通过的电流 | |
| D. | K断开,a、c两灯立即熄灭. |
12.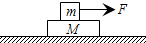 如图所示,质量为M的长木板位于光滑水平面上,质量为m的物块静止在长木板上,两者之间的滑动摩擦因数为μ,现对物块m施加水平向右的恒力F,若恒力F超过某一临界数值,长木板与物块将出现相对滑动.重力加速度大小为g,物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力.则恒力F的临界数值为( )
如图所示,质量为M的长木板位于光滑水平面上,质量为m的物块静止在长木板上,两者之间的滑动摩擦因数为μ,现对物块m施加水平向右的恒力F,若恒力F超过某一临界数值,长木板与物块将出现相对滑动.重力加速度大小为g,物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力.则恒力F的临界数值为( )
 如图所示,质量为M的长木板位于光滑水平面上,质量为m的物块静止在长木板上,两者之间的滑动摩擦因数为μ,现对物块m施加水平向右的恒力F,若恒力F超过某一临界数值,长木板与物块将出现相对滑动.重力加速度大小为g,物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力.则恒力F的临界数值为( )
如图所示,质量为M的长木板位于光滑水平面上,质量为m的物块静止在长木板上,两者之间的滑动摩擦因数为μ,现对物块m施加水平向右的恒力F,若恒力F超过某一临界数值,长木板与物块将出现相对滑动.重力加速度大小为g,物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力.则恒力F的临界数值为( )| A. | μmg | B. | μMg | C. | μmg(1+$\frac{m}{M}$) | D. | μmg(1+$\frac{M}{m}$) |
13.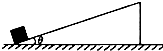 一物块以初速度v0冲上倾角为θ且足够长的固定斜面,经过t时间到达最高点;又经过2t时间回到出发点,已知重力加速度为g,根据以上信息可以求出( )
一物块以初速度v0冲上倾角为θ且足够长的固定斜面,经过t时间到达最高点;又经过2t时间回到出发点,已知重力加速度为g,根据以上信息可以求出( )
 一物块以初速度v0冲上倾角为θ且足够长的固定斜面,经过t时间到达最高点;又经过2t时间回到出发点,已知重力加速度为g,根据以上信息可以求出( )
一物块以初速度v0冲上倾角为θ且足够长的固定斜面,经过t时间到达最高点;又经过2t时间回到出发点,已知重力加速度为g,根据以上信息可以求出( )| A. | 物块的质量 | B. | 物块与斜面之间的动摩擦因数 | ||
| C. | 物块的末速度 | D. | 物块的末动能 |
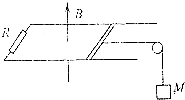 如图,竖直向上的匀强磁场的磁感应强度为B,水平导轨不计电阻,且不计摩擦,宽为s,在导轨上搁一根质量为m、电阻为R0的导体棒,棒与导轨接触良好,且用水平细线通过定滑轮吊着质量为M的重物,导轨上还连着阻值为R电阻,现让重物从静止开始下落.
如图,竖直向上的匀强磁场的磁感应强度为B,水平导轨不计电阻,且不计摩擦,宽为s,在导轨上搁一根质量为m、电阻为R0的导体棒,棒与导轨接触良好,且用水平细线通过定滑轮吊着质量为M的重物,导轨上还连着阻值为R电阻,现让重物从静止开始下落.