题目内容
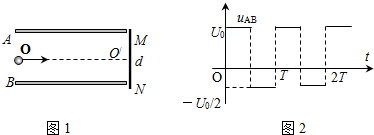
如图1所示,水平放置长为L的平行金属板A和B的距离为d,它们的右端安放着垂直于金属板的靶MN,现在A、B板上加上如图2所示的方波电压,电压的正向值为U0,反向电压值为
,且每隔
换向一次,现有质量为m、带正电且电量为q的粒子束从A、B的中点O沿平行于金属板方向OO′射入,设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T.不计重力的影响,试问:
(1)在靶MN上距其中心O′点多远的范围内有粒子击中?
(2)要使粒子能全部打在靶MN上,电压U0的数值应满足什么条件?(写出U0、m、d、q、T的关系式即可)
(3)求打在靶上的粒子的速度有多大?
| U0 |
| 2 |
| T |
| 2 |
(1)在靶MN上距其中心O′点多远的范围内有粒子击中?
(2)要使粒子能全部打在靶MN上,电压U0的数值应满足什么条件?(写出U0、m、d、q、T的关系式即可)
(3)求打在靶上的粒子的速度有多大?

分析:1、由运动的独立性可知,带电粒子在水平方向做匀速直线运动,竖直方向在电场力的作用下做变速运动.粒子打在靶MN上的范围,实际上就是粒子在竖直方向所能到达的范围.分别计算当粒子在0,T,2T,…nT时刻进入电场中和粒子在
,3
,…(2n+1)
时刻进入电场时,这两种情况向粒子在竖直方向上的位移.比较哪个最大,最大是多少.
2、要使粒子能全部打在靶上,竖直方向上最大位移必须小于
,列式化简即可.
3、根据动量定理,求解垂直于极板的速度度为Vy,在平行于极板方向做匀速直线运动,所以平行于极板的速度v0=
,根据勾股定理v=
计算打在靶上的粒子的速度.
| T |
| 2 |
| T |
| 2 |
| T |
| 2 |
2、要使粒子能全部打在靶上,竖直方向上最大位移必须小于
| d |
| 2 |
3、根据动量定理,求解垂直于极板的速度度为Vy,在平行于极板方向做匀速直线运动,所以平行于极板的速度v0=
| L |
| T |
| v02+vy2 |
解答:解:由运动的独立性可知,带电粒子在水平方向做匀速直线运动,竖直方向在电场力的作用下做变速运动.粒子打在靶MN上的范围,实际上就是粒子在竖直方向所能到达的范围.
(1)当粒子在0,T,2T,…nT时刻进入电场中时,粒子将打在O′点下方最远点,在前
时间内,粒子在竖直向下的位移为:
s1=
a1(
)2=
在后
时间内,粒子在竖直向下的位移为:s2=v?
-
a2(
)2
将v=a1
=
,a2=
代入上式得:s2=
故粒子打在距O′点正下方的最大位移为:s=s1+s2=
当粒子在
,3
,…(2n+1)
时刻进入电场时,将打在O′点上方最远点,在前
时间内,粒子在竖直向上的位移为:
s1′=
a1′(
)2=
(
)2=
在后
时间内,粒子在竖直向上的位移为:s2′=v′
-
a2′(
)2
其中,v′=a1′
=
,a2′=
,代入上式得:s2′=0,
故粒子打在距O′点正上方的最大位移为:s′=s1′+s2′=
.
(2)要使粒子能全部打在靶上,须有:
<
,即U0<
.
(3)因为粒子在平行于极板方向做匀速直线运动,所以平行于极板的速度:
v0=
设垂直于极板的速度度为Vy,则据动量定理有:
mvy=
-
=
T
所以打在靶上粒子的速度为v=
=
答:(1)故粒子打在距O′点正上方的最大位移为:
.
(2)要使粒子能全部打在靶MN上,电压U0的数值应满足U0<
.
(3)打在靶上的粒子的速度为
.
(1)当粒子在0,T,2T,…nT时刻进入电场中时,粒子将打在O′点下方最远点,在前
| T |
| 2 |
s1=
| 1 |
| 2 |
| T |
| 2 |
| qU0T2 |
| 8md |
在后
| T |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
将v=a1
| T |
| 2 |
| qU0 |
| 2md |
| qU0 |
| 2md |
| 3qU0T2 |
| 16md |
故粒子打在距O′点正下方的最大位移为:s=s1+s2=
| 5qU0T2 |
| 16md |
当粒子在
| T |
| 2 |
| T |
| 2 |
| T |
| 2 |
| T |
| 2 |
s1′=
| 1 |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
| qU0 |
| md |
| T |
| 2 |
| qU0T2 |
| 16md |
在后
| T |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
其中,v′=a1′
| T |
| 2 |
| qU0T |
| 4md |
| qU0 |
| md |
故粒子打在距O′点正上方的最大位移为:s′=s1′+s2′=
| qU0T2 |
| 16md |
(2)要使粒子能全部打在靶上,须有:
| 5qU0T2 |
| 16md |
| d |
| 2 |
| 8md2 |
| 5qT2 |
(3)因为粒子在平行于极板方向做匀速直线运动,所以平行于极板的速度:
v0=
| L |
| T |
设垂直于极板的速度度为Vy,则据动量定理有:
mvy=
| qU0 |
| d |
| T |
| 2 |
| qU0 |
| 2d |
| T |
| 2 |
| 1 |
| 4 |
| qU0 |
| d |
所以打在靶上粒子的速度为v=
| v02+vy2 |
|
答:(1)故粒子打在距O′点正上方的最大位移为:
| qU0T2 |
| 16md |
(2)要使粒子能全部打在靶MN上,电压U0的数值应满足U0<
| 8md2 |
| 5qT2 |
(3)打在靶上的粒子的速度为
|
点评:本题是带电粒子在电场中的偏转,是典型的类平抛运动的问题,把粒子的运动分解为水平和竖直方向上的运动,在水平方向上做匀速运动,竖直方向上做匀速直线运动,本题还要注意电场力的大小和方向具有周期.

练习册系列答案
相关题目
 (2012?静安区一模)如图1所示,水平放置的均匀玻璃管内,一段长为h=25cm的水银柱封闭了长为L0=20cm、温度为t0=27℃的理想气体,大气压强P0=75cmHg.将玻璃管缓慢地转过90°角,使它开口向上,并将封闭端浸入热水中(如图2),待稳定后,测得玻璃管内封闭气柱
(2012?静安区一模)如图1所示,水平放置的均匀玻璃管内,一段长为h=25cm的水银柱封闭了长为L0=20cm、温度为t0=27℃的理想气体,大气压强P0=75cmHg.将玻璃管缓慢地转过90°角,使它开口向上,并将封闭端浸入热水中(如图2),待稳定后,测得玻璃管内封闭气柱
 如图1所示,水平放置的汽缸内壁光滑,活塞的厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,A左侧汽缸的容积为V0,A、B之间容积为0.1V0,开始时活塞在A处,缸内气体压强为0.9P0(P0为大气压强),温度为297K,现通过对气体缓慢加热使活塞恰好移动到B,求:
如图1所示,水平放置的汽缸内壁光滑,活塞的厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,A左侧汽缸的容积为V0,A、B之间容积为0.1V0,开始时活塞在A处,缸内气体压强为0.9P0(P0为大气压强),温度为297K,现通过对气体缓慢加热使活塞恰好移动到B,求: