题目内容
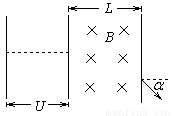
电视机显像管简单原理如图所示，初速度不计的电子经加速电场加速后进入有限边界宽度为L的匀强磁场，磁感应强度为B，如要求电子束偏转角为α，已知电子电量为e，质量为m．（1）画出整个过程的轨迹图；
（2）电子在磁场中运动的时间；
（3）求加速电场的电势差U．
分析：（1）根据电场力与洛伦兹力方向，结合力与运动的关系，从而即可求解；
（2）根据电子的运动周期，结合圆心角，即可求解；
（3）根据动能定理与牛顿第二定律，结合几何关系，即可求解．
（2）根据电子的运动周期，结合圆心角，即可求解；
（3）根据动能定理与牛顿第二定律，结合几何关系，即可求解．
解答：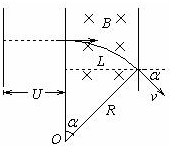
解：（1）电子现在加速电场中做匀加速直线运动，然后进入匀强磁场中作匀速圆周运动，轨迹如图；
（2）根据电子做匀速圆周运动，则运动时间：t=
由T=
解得：t=
；
（3）电子经加速电场加速后，速度为v，
则由动能定理得：eU=
mv2；
由几何关系得，电子运动半径：R=
；
由牛顿第二定律，有：evB=
；
由以上各式解得加速电压：U=
；
答：（1）画出整个过程的轨迹图如上所示；
（2）电子在磁场中运动的时间t=
；
（3）求加速电场的电势差U=
．
解：（1）电子现在加速电场中做匀加速直线运动，然后进入匀强磁场中作匀速圆周运动，轨迹如图；（2）根据电子做匀速圆周运动，则运动时间：t=
| αT |
| 2π |
由T=
| 2πm |
| eB |
解得：t=
| αm |
| eB |
（3）电子经加速电场加速后，速度为v，
则由动能定理得：eU=
| 1 |
| 2 |
由几何关系得，电子运动半径：R=
| L |
| sinα |
由牛顿第二定律，有：evB=
| mv2 |
| R |
由以上各式解得加速电压：U=
| eB2L2 |
| 2msin2α |
答：（1）画出整个过程的轨迹图如上所示；
（2）电子在磁场中运动的时间t=
| αm |
| eB |
（3）求加速电场的电势差U=
| eB2L2 |
| 2msin2α |
点评：考查粒子在电场中加速与磁场中偏转，掌握动能定理与牛顿第二定律的应用，注意运动半径与已知长度的关系，同时由几何关系确定圆心角是解题的关键．
练习册系列答案
相关题目
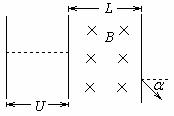
电视机显像管简单原理如图所示，初速度不计的电子经加速电场加速后进入有限边界宽度为L的匀强磁场，磁感应强度为B，如要求电子束偏转角为α，求加速电场的电势差U．（已知电子电量为e，质量为m）
，求加速电场的电势差U。（已知电子电量为e，质量为m）
，求加速电场的电势差U。（已知电子电量为e，质量为m）
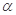，求加速电场的电势差U。（已知电子电量为e，质量为m）