题目内容
【题目】如图，某种材料制成的三角形棱镜ABC，其中∠A=53°，∠B=90°，在棱镜右侧距离BC边为d处有一竖直光屏MN，已知AC=4d，E为AC上的一点，且AE=4EC，O点为C点在光屏上的投影。现有a、b两种单色光组成的细光束，从E点垂直AC边射入棱镜，已知棱镜对a光的折射率n1=
，对b光的折射率为n2=
．光在真空中的传播速度为c，不考虑a光在棱镜中的反射，sin53°=0.8．求：
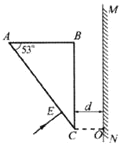
①射到光屏MN上的光点到O点的距离；
②a光在棱镜中传播的时间。
【答案】①射到光屏MN上的光点到O点的距离是
d；②a光在棱镜中传播的时间是
。
【解析】
①画出光路图如图所示，在界面BC发生折射时，入射角为i，折射角分别为ra、rb，
由折射定律得：
=
，
=
由几何关系知：i=37°
解得：sinra=0.8，sinra=1，ra=90°
说明b光在BC边上发生了全反射
EC=
AC=
d，FC=
=d
a光射到光屏MN上的光点到O点的距离分别为
HO=FC+dtanra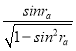=d+d
=d+d
=
d
②a光在棱镜中传播的距离s=ECtan37°=
d
a光在棱镜中传播的速度v=
=
c
故a光在棱镜中传播的时间为t=
=
练习册系列答案
相关题目
