题目内容
2. 某短跑运动员参加100m竞赛,用时10s,测得他在5s末的速度为10m/s,在10s末的速度为10.8m/s,此运动员在这100m中的平均速度为10m/s,设想此运动员在前5s做匀加速直线运动,则他的加速度为2m/s2,请你在如图所给的虚线框内画出此运动员的v-t图象.
某短跑运动员参加100m竞赛,用时10s,测得他在5s末的速度为10m/s,在10s末的速度为10.8m/s,此运动员在这100m中的平均速度为10m/s,设想此运动员在前5s做匀加速直线运动,则他的加速度为2m/s2,请你在如图所给的虚线框内画出此运动员的v-t图象.
分析 根据短跑运动员的位移和运动的时间,结合平均速度的定义式求出运动员在这100m中的平均速度,根据匀加速直线运动速度时间公式求出加速度,根据运动情况画出v-t图象.
解答 解:运动员在这100m中的平均速度为$\overline{v}=\frac{x}{t}=\frac{100}{10}=10m/s$,
若运动员在前5s做匀加速直线运动,根据v=at得:a=$\frac{10}{5}=2m/{s}^{2}$,此运动员前5s做匀加速直线运动,后5s做变加速运动,v-t图象如图所示:
故答案为:10;2;如图所示.
点评 解决本题的关键掌握平均速度的定义式,不要受运动过程瞬时速度的干扰,抓住总位移和总时间求出平均速度,能根据匀变速直线运动基本公式求解加速度.

练习册系列答案
相关题目
12. 电子束以一定的初速度沿轴线进入螺线管内,螺线管中通以方向随时间而周期性变化的电流,如图所示,则电子束在螺线管中做( )
电子束以一定的初速度沿轴线进入螺线管内,螺线管中通以方向随时间而周期性变化的电流,如图所示,则电子束在螺线管中做( )
 电子束以一定的初速度沿轴线进入螺线管内,螺线管中通以方向随时间而周期性变化的电流,如图所示,则电子束在螺线管中做( )
电子束以一定的初速度沿轴线进入螺线管内,螺线管中通以方向随时间而周期性变化的电流,如图所示,则电子束在螺线管中做( )| A. | 匀速直线运动 | B. | 匀速圆周运动 | ||
| C. | 加速减速交替的运动 | D. | 来回振动 |
5.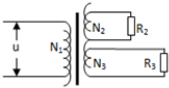 图中所示是一理想变压器的示意图,铁芯上绕有3个线圈,1为原线圈,2、3为副线圈,它们的匝数之间比为N1 :N2 :N3 =10:2:1,设三个线圈的绕线电阻均可忽略,副线圈2、3上分别接有阻值为8Ω和4Ω的负载电阻R2的R3,现在原线圈1上加上:u=20$\sqrt{2}$ sin100πt (V)的交变电压,则( )
图中所示是一理想变压器的示意图,铁芯上绕有3个线圈,1为原线圈,2、3为副线圈,它们的匝数之间比为N1 :N2 :N3 =10:2:1,设三个线圈的绕线电阻均可忽略,副线圈2、3上分别接有阻值为8Ω和4Ω的负载电阻R2的R3,现在原线圈1上加上:u=20$\sqrt{2}$ sin100πt (V)的交变电压,则( )
 图中所示是一理想变压器的示意图,铁芯上绕有3个线圈,1为原线圈,2、3为副线圈,它们的匝数之间比为N1 :N2 :N3 =10:2:1,设三个线圈的绕线电阻均可忽略,副线圈2、3上分别接有阻值为8Ω和4Ω的负载电阻R2的R3,现在原线圈1上加上:u=20$\sqrt{2}$ sin100πt (V)的交变电压,则( )
图中所示是一理想变压器的示意图,铁芯上绕有3个线圈,1为原线圈,2、3为副线圈,它们的匝数之间比为N1 :N2 :N3 =10:2:1,设三个线圈的绕线电阻均可忽略,副线圈2、3上分别接有阻值为8Ω和4Ω的负载电阻R2的R3,现在原线圈1上加上:u=20$\sqrt{2}$ sin100πt (V)的交变电压,则( )| A. | 通过原线圈3上的交变电流i3=0.5 sin100πt (A) | |
| B. | 通过副线圈2和副线圈3的电流之比为1:1 | |
| C. | R2上一分钟内产生的焦耳热为240J | |
| D. | 当R2电阻变为原来二倍时通过原线圈的电流有效值也随之减小为原来的$\frac{1}{2}$ |
9. 在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )
在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )
 在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )
在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )| A. | 物块c的质量是2msinθ | |
| B. | b棒放上导轨前,物块c减少的重力势能等于a、c增加的动能 | |
| C. | b棒放上导轨后,物块c减少的重力势能等于回路消耗的电能 | |
| D. | b棒放上导轨后,a棒中电流大小是$\frac{mgcosθ}{BL}$ |
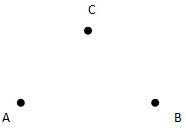 如图所示,A、B、C为匀强电场中的3个点,已知这3点的电势分别为ϕA=10V,ϕB=2V,ϕC=-6V.试在图上画出过B点的等势线和场强的方向(用刻度尺画图).一个电子从A到B再到C做功为-8eV.
如图所示,A、B、C为匀强电场中的3个点,已知这3点的电势分别为ϕA=10V,ϕB=2V,ϕC=-6V.试在图上画出过B点的等势线和场强的方向(用刻度尺画图).一个电子从A到B再到C做功为-8eV. 如图是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道.表演者骑着摩托车在圆轨道内做圆周运动.已知人和摩托车的总质量为m,人以v1=$\sqrt{2gR}$的速度过轨道最高点B,并以v2=$\sqrt{3}$v1的速度过最低点A.求在A、B两点,轨道对摩托车的压力大小相差多少?(g为重力加速度)
如图是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道.表演者骑着摩托车在圆轨道内做圆周运动.已知人和摩托车的总质量为m,人以v1=$\sqrt{2gR}$的速度过轨道最高点B,并以v2=$\sqrt{3}$v1的速度过最低点A.求在A、B两点,轨道对摩托车的压力大小相差多少?(g为重力加速度) 如图所示一块长为L=2m高为H=45cm质量为M=2kg的长方体木块静止在水平地面上,一个质量为m=0.5kg的四驱车(四轮驱动)从木块的最左端由静止开始以大小恒定的加速度a=6m/s2向右加速运动.(可以把四驱车看成质点)
如图所示一块长为L=2m高为H=45cm质量为M=2kg的长方体木块静止在水平地面上,一个质量为m=0.5kg的四驱车(四轮驱动)从木块的最左端由静止开始以大小恒定的加速度a=6m/s2向右加速运动.(可以把四驱车看成质点) 如图所示,飞机离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度v2=20m/s同向行驶的汽车,欲使从飞机上投下的炸弹击中汽车,飞机应在距汽车水平距离800m处投弹.(g=10m/s2)
如图所示,飞机离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度v2=20m/s同向行驶的汽车,欲使从飞机上投下的炸弹击中汽车,飞机应在距汽车水平距离800m处投弹.(g=10m/s2)