题目内容
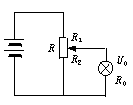
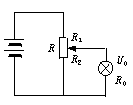
 如图所示,用电动势E=6V,内阻不计的蓄电池通过滑动变阻器组成分压电路,向电阻R0=20Ω,额定电压U0=4.5V的灯泡供电,试问:
如图所示,用电动势E=6V,内阻不计的蓄电池通过滑动变阻器组成分压电路,向电阻R0=20Ω,额定电压U0=4.5V的灯泡供电,试问:(1)当电池组对灯泡的供电效率(即电灯功率与电源总功率之比)η0=60%时,变阻器R的阻值和应承受的最大电流是多少?
(2)采用图中电源和变阻器对处于额定电压的灯泡供电时,最大效率是多少?
分析:(1)先根据串联并联电路的特点,得出R1与R2的关系,再根据效率等于有用功率与总功率之比,列式求解变阻器R的阻值.再由欧姆定律得到能承受的最大电流.
(2)电源的效率η=
=
,R是外电路总电阻,当R2的阻值越大时,并联部分分担的电压越大,电源的效率越大,R2断路时,系统有最大可能效率.
(2)电源的效率η=
| UI |
| EI |
| R0 |
| R |
解答:解:(1)由题意,灯泡正常发光,U0=4.5V,电源的内阻不计,则R1的电压为U1=E-U0=6V-4.5V=1.5V
根据串联并联电路的特点,得:
=
代入数据得:
=
…①
根据效率为η=60%得:η=
代入得:60%=
…②
联立①②得:R1=5
Ω,R2=80Ω
则得:R=R1+R2=85
Ω
当所以变阻器的总电阻:R=85
Ω≈85.3Ω,
它应承受的电流是:I=
=
A=0.281A
(2)当R2的阻值越大,并联部分分担的电压越大,电源的效率越大,则当R2→∞时,即R2断路时,系统有最大可能的效率ηmax
故最大效率ηmax=
×100%=
×100%=
×100%=75%.
答:
(1)当电池组对灯泡的供电效率(即电灯功率与电源总功率之比)η0=60%时,变阻器R的阻值为85.3Ω,应承受的最大电流是0.281A.
(2)采用图中电源和变阻器对处于额定电压的灯泡供电时,最大效率是75%.
根据串联并联电路的特点,得:
| U1 |
| U0 |
| R1 | ||
|
代入数据得:
| 1.5 |
| 4.5 |
| R1(R2+20) |
| 20R2 |
根据效率为η=60%得:η=
| ||||||||||||
|
代入得:60%=
| ||||||
|
联立①②得:R1=5
| 1 |
| 3 |
则得:R=R1+R2=85
| 1 |
| 3 |
当所以变阻器的总电阻:R=85
| 1 |
| 3 |
它应承受的电流是:I=
| U1 |
| R1 |
| 1.5 | ||
|
(2)当R2的阻值越大,并联部分分担的电压越大,电源的效率越大,则当R2→∞时,即R2断路时,系统有最大可能的效率ηmax
故最大效率ηmax=
| U0I |
| EI |
| U0 |
| E |
| 4.5 |
| 6 |
答:
(1)当电池组对灯泡的供电效率(即电灯功率与电源总功率之比)η0=60%时,变阻器R的阻值为85.3Ω,应承受的最大电流是0.281A.
(2)采用图中电源和变阻器对处于额定电压的灯泡供电时,最大效率是75%.
点评:本题关键要根据电路结构,运用欧姆定律和功率公式列式,组成方程组求解.

练习册系列答案
相关题目
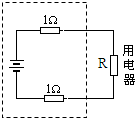 如图所示,用电动势为E=8V,内电阻r=2Ω的电池连接两根各1Ω的电阻线组成电源(虚线框内部分),向某用电器R(纯电阻)供电,该用电器可获得P=3W的电功率.求通过该用电器的电流和它两端的电压.
如图所示,用电动势为E=8V,内电阻r=2Ω的电池连接两根各1Ω的电阻线组成电源(虚线框内部分),向某用电器R(纯电阻)供电,该用电器可获得P=3W的电功率.求通过该用电器的电流和它两端的电压.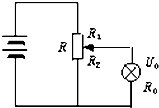 如图所示,用电动势E=6V,内阻不计的蓄电池组,通过滑线变阻器组成分压电路,当电阻R0=20Ω,额定电压U0=4.5V的灯泡供电使它正常发光,试问当电池组对灯泡的供电效率η=60%时,变阻器R的阻值和能承受的最大电流应满足什么要求?
如图所示,用电动势E=6V,内阻不计的蓄电池组,通过滑线变阻器组成分压电路,当电阻R0=20Ω,额定电压U0=4.5V的灯泡供电使它正常发光,试问当电池组对灯泡的供电效率η=60%时,变阻器R的阻值和能承受的最大电流应满足什么要求?