题目内容
如图所示,在光滑的水平面上,停着质量为M、长为L的小车,一个质量为m的滑块从车内底板的正中央获得大小为v0的速度后向车壁运动,若滑块与车底板之间的动摩擦因数为μ,滑块与车壁之间的碰撞没有能量损失,求滑块与车壁的碰撞次数.


以滑块与车壁组成的系统为研究对象,设滑块与车相对时共同速度为v,则由动量守恒定律得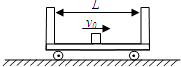
mv0=(M+m)v
得到v=
设滑块相对于车滑动的总路程为s,则由能量守恒定律得
μmgs=
mv02-
(M+m)v2
得到s=
滑块与车壁的碰撞次数为n=1+
代入解得n=
+
答:滑块与车壁的碰撞次数n=
+
.

mv0=(M+m)v
得到v=
| mv0 |
| M+m |
设滑块相对于车滑动的总路程为s,则由能量守恒定律得
μmgs=
| 1 |
| 2 |
| 1 |
| 2 |
得到s=
M
| ||
| 2(M+m)μg |
滑块与车壁的碰撞次数为n=1+
s-
| ||
| L |
代入解得n=
| Mv02 |
| 2μ(M+m)gL |
| 1 |
| 2 |
答:滑块与车壁的碰撞次数n=
| Mv02 |
| 2μ(M+m)gL |
| 1 |
| 2 |

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目