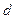题目内容
长为L的轻绳一端系一小球，另一端悬于O点。小球从与竖直方向成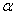
角处释放，到最低点与一钉子C相碰后绕C做圆周运动，若半径
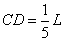，欲使小球刚好能通过最高点，则
（1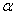）角应为多大？
（2）若小球释放位置不变，则到达最低点时碰钉子后瞬间绳子对小球的拉力等于多大？
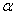角处释放，到最低点与一钉子C相碰后绕C做圆周运动，若半径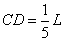，欲使小球刚好能通过最高点，则（1）
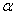角应为多大？（2）若小球释放位置不变，则到达最低点时碰钉子后瞬间绳子对小球的拉力等于多大？
14分）解：（1）（7分）从A→D过程中，
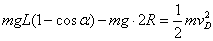
在D处，由于小球刚好能通过最高点，则有
其中
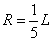
解以上方程得：
2）（7分）从A→B，由机械能守恒有
在B处受力如图，由牛顿第二定律
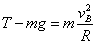其中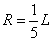
解得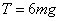
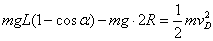
在D处，由于小球刚好能通过最高点，则有
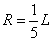
其中解以上方程得：
2）（7分）从A→B，由机械能守恒有
在B处受力如图，由牛顿第二定律
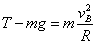其中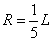解得
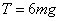
略
练习册系列答案
相关题目
；两个物体均可视为质点，不计绳子和滑轮的质量、不计滑轮轴上的摩擦力和空气阻力。问：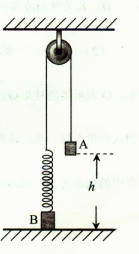
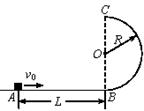
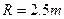的竖直半圆轨道组成，现由水平地面上的A点斜向上抛出一个小球，使之由半圆轨道的最高点B水平进入轨道，沿轨道运动，已知小球冲上弧形轨道的最大高度为
，
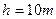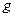取
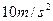。求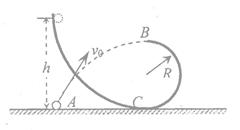
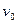的大小和方向