题目内容
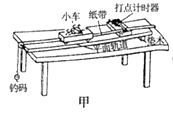
【题目】一轻弹簧的一端固定在倾角为![]() 的固定光滑斜面的底部,另一端和质量为m的小物块a相连,如图所示
的固定光滑斜面的底部,另一端和质量为m的小物块a相连,如图所示![]() 质量为
质量为![]() 的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为
的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为![]() ,从t=0时开始,对b施加沿斜面向上的外力,使b始终做匀加速直线运动
,从t=0时开始,对b施加沿斜面向上的外力,使b始终做匀加速直线运动![]() 经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为
经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为![]() ,弹簧的形变始终在弹性限度内,重力加速度大小为
,弹簧的形变始终在弹性限度内,重力加速度大小为![]() ,求
,求

(1)弹簧的劲度系数;
(2)物块b加速度的大小;
(3)在物块a、b分离前,外力大小随时间变化的关系式.
【答案】(1)弹簧的劲度系数为![]() ;
;
(2)物块b加速度的大小为![]() ;
;
(3)在物块a、b分离前,外力大小随时间变化的关系式![]()
【解析】(1)对整体分析,根据平衡条件可知,沿斜面方向上重力的分力与弹簧弹力平衡,则有:
kx0=(m+![]() m)gsinθ
m)gsinθ
解得:k=![]()
(2)由题意可知,b经两段相等的时间位移为x0;
由匀变速直线运动相邻相等时间内位移关系的规律可知:![]()
说明当形变量为![]() 时二者分离;
时二者分离;
对m分析,因分离时ab间没有弹力,则根据牛顿第二定律可知:kx1-mgsinθ=ma
联立解得:a=![]()
(3)设时间为t,则经时间t时,ab前进的位移x=![]() at2=
at2=![]()
则形变量变为:△x=x0-x
对整体分析可知,由牛顿第二定律有:F+k△x-(m+![]() m)gsinθ=(m+
m)gsinθ=(m+![]() m)a
m)a
解得:F=![]() mgsinθ+
mgsinθ+![]() t2
t2
因分离时位移x=![]() 由x=
由x=![]() =
=![]() at2解得:
at2解得:![]()
故应保证0≤t<![]() ,F表达式才能成立.
,F表达式才能成立.

练习册系列答案
相关题目