题目内容
18.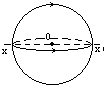 如图所示,两个半径相同、粗细相同互相垂直的圆形导线圈,可以绕通过公共的轴线xx′自由转动,分别通以相等的电流,设每个线圈中电流在圆心处产生磁感应强度为B,当两线圈转动而达到平衡时,圆心O处的磁感应强度大小是( )
如图所示,两个半径相同、粗细相同互相垂直的圆形导线圈,可以绕通过公共的轴线xx′自由转动,分别通以相等的电流,设每个线圈中电流在圆心处产生磁感应强度为B,当两线圈转动而达到平衡时,圆心O处的磁感应强度大小是( )| A. | 1B | B. | $\sqrt{2}$B | C. | 2B | D. | 0 |
分析 该题是关于磁场的叠加问题.首先运用安培定则每个圆环在圆心O处产生的磁感应强度的方向,利用平行四边形定则进行矢量合成,即求出O处的磁感应强度大小.
解答 解:根据安培定则可知,竖直方向的通电圆环在圆心O处产生的磁感应强度方向垂直纸面向里,大小为B,水平方向的通电圆环在圆心O处产生的磁感应强度方向竖直向上,大小为B,两者相互垂直,由于同向电流吸引,两个线圈重合,故当两线圈转动而达到重合时,圆心O处的磁感强度的大小是BO=2B.
故选:C
点评 本题的解题关键是掌握安培定则,并能熟练应用,同时要能正确运用平行四边形定则进行矢量合成.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
8.下列图象属于匀变速直线运动的是( )
| A. |  | B. | 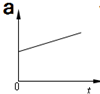 | C. | 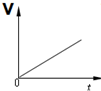 | D. |  |
13.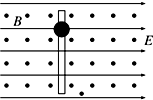 如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电荷量为q,小球可在棒上滑动.现将此棒竖直放入沿水平方向且互相垂直的匀强磁场和匀强电场中,设小球电荷量不变,在小球由静止下滑的过程中( )
如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电荷量为q,小球可在棒上滑动.现将此棒竖直放入沿水平方向且互相垂直的匀强磁场和匀强电场中,设小球电荷量不变,在小球由静止下滑的过程中( )
 如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电荷量为q,小球可在棒上滑动.现将此棒竖直放入沿水平方向且互相垂直的匀强磁场和匀强电场中,设小球电荷量不变,在小球由静止下滑的过程中( )
如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电荷量为q,小球可在棒上滑动.现将此棒竖直放入沿水平方向且互相垂直的匀强磁场和匀强电场中,设小球电荷量不变,在小球由静止下滑的过程中( )| A. | 小球加速度一直增大 | |
| B. | 小球速度一直增大,直到最后匀速 | |
| C. | 小球速度先增大,再减小,直到停止运动 | |
| D. | 杆对小球的弹力一直减小 |
3.2012年8月12日,在伦敦奥运会男子拳击49公斤级决赛中,中国名将邹市明发挥出色,以13-10险胜泰国高手庞普里亚杨夺得金牌,成功卫冕.下列说法中,正确的是( )
| A. | 邹市明没有受到力的作用 | B. | 邹市明只是施力者 | ||
| C. | 双方既是受力者,也是施力者 | D. | 对方只能是受力者 |
10.关于静电场,下列说法正确的是( )
| A. | 电势等于零的物体一定不带电 | |
| B. | 电场强度为零的点,电势一定为零 | |
| C. | 同一电场线上的各点,电势一定不相等 | |
| D. | 负电荷沿电场线方向移动时,电势能一定增加 |
5.一个物体正在做匀速圆周运动,下列说法中正确的是( )
| A. | 它的速度不变 | B. | 它的加速度不变 | ||
| C. | 它所受的合力一直在变化 | D. | 它所受的合力不变 |
6. 如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,下列结论中正确的是( )
如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,下列结论中正确的是( )
 如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,下列结论中正确的是( )
如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,下列结论中正确的是( )| A. | 物体到达各点的速率vB:vC:vD:vE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 物体到达各点所经历的时间:tC=$\frac{1}{2}$tE | |
| C. | 物体从A到E的平均速度$\overline{v}$=$\frac{\sqrt{2}}{2}$vC | |
| D. | 物体通过每一部分时,其速度增量vB-vA=vC-vB=vD-vC=vE-vD |
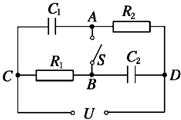 如图所示,电容器C1=6 μF,C2=3 μF,电阻R1=6Ω,R2=3Ω,U=18V,则:
如图所示,电容器C1=6 μF,C2=3 μF,电阻R1=6Ω,R2=3Ω,U=18V,则: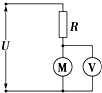 如图所示是一提升重物用的直流电动机工作时的电路图.电动机内电阻r=0.8Ω,电路中另一电阻R=8Ω,直流电压U=160V,理想电压表示数UV=120V.试求:
如图所示是一提升重物用的直流电动机工作时的电路图.电动机内电阻r=0.8Ω,电路中另一电阻R=8Ω,直流电压U=160V,理想电压表示数UV=120V.试求: