题目内容
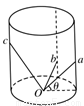
如图所示，圆柱形的仓库内有三块长度不同的滑板aO、bO、cO，其下端都固定于底部圆心O，而上端则搁在仓库侧壁上，三块滑板与水平面的夹角依次是30°、45°、60°，若有三个质量相同的小孩从a、b、c处下滑到O点的过程中（忽略阻力），则（ ）分析：研究斜面是任意角时滑环运动到D所用的时间，由牛顿第二定律得到滑环的加速度，由位移公式得到时间与斜面倾角的关系，由数学知识分析时间的关系．
解答：解：A、B、C、设OD=d，任意一斜面的倾角为α，则由牛顿第二定律得到滑环的加速度为 a=gsinα，滑环从斜面的顶点滑到D的位移为 x=
．
由x=
at2得，t=
=
=
由数学知识得知，sin（2×60°）=sin（2×30°），sin（2×45°）=1最大，即b运动时间最短，a、c运动时间最长且相等；
由于重力相同，故重力对a、c的冲量相等，对b的冲量最大；故AB正确，C错误；
D、支持力N=mgcosα，三个小孩受到的支持力全不同，故支持力冲量不等，故D错误；
故选AB．
| d |
| cosα |
由x=
| 1 |
| 2 |
|
|
| 4d |
| g?sin2α |
由数学知识得知，sin（2×60°）=sin（2×30°），sin（2×45°）=1最大，即b运动时间最短，a、c运动时间最长且相等；
由于重力相同，故重力对a、c的冲量相等，对b的冲量最大；故AB正确，C错误；
D、支持力N=mgcosα，三个小孩受到的支持力全不同，故支持力冲量不等，故D错误；
故选AB．
点评：本题是牛顿第二定律和运动学公式的综合应用，关键要抓住三个过程相同的量表示位移和加速度．
练习册系列答案
考前必练系列答案
相关题目
如图所示，圆柱形的仓库内有三块长度不同的滑板aO、bO、cO，其下端都固定于底部圆心O，而上端则搁在仓库侧壁上，三块滑板与水平面的夹角依次是30°、45°、60°．若有三个小孩同时从a、b、c处开始下滑（忽略阻力）则（ ）
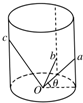如图所示，圆柱形的仓库内有三块长度不同的滑板aO、bO、cO，其下端都固定于底部圆心O，而上端则搁在仓库侧壁上，三块滑板与水平面的夹角依次是30°、45°、60°．若有三个小孩同时从a、b、c处开始下滑（忽略阻力），则（ ）| A、a处小孩最先到O点 | B、b处小孩最先到O点 | C、c处小孩最先到O点 | D、三个小孩同时到O点 |
