题目内容
（2009?宜昌模拟）如图所示，质量m=1kg的小球套在足够长的细杆上，细杆与水平方向成α=30°角，球与杆之间的动摩擦因数μ=
| ||
| 6 |
（1）小球的加速度的大小；
（2）若2秒后撤去外力F，小球沿杆运动离出发点的最远距离是多少．
分析：（1）对小球进行受力分析，根据正交分解，运用牛顿第二定律求出小球的加速度．
（2）根据匀变速直线运动的公式求出前2s内的位移和2s末的速度；根据牛顿第二定律求出撤去外力后的加速度，运用运动学公式求出匀减速直线运动的位移，从而得出小球沿杆运动离出发点的最远距离．
（2）根据匀变速直线运动的公式求出前2s内的位移和2s末的速度；根据牛顿第二定律求出撤去外力后的加速度，运用运动学公式求出匀减速直线运动的位移，从而得出小球沿杆运动离出发点的最远距离．
解答：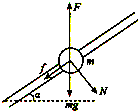
解：（1）对小球受力分析如图，则有：
Fsinα-f-mgsinα=ma
FN+mgcosα=Fcosα
F=μFN
联立三式解得a=2.5m/s2
答：小球的加速度的大小为a=2.5m/s2．
（2）2s内物体的位移
s1=
at2=5m
2s末物体的速度
v=at=5m/s
撤去力F后，物体受力如图所示，则有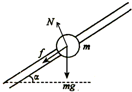
μmgcosα+mgsinα=ma′
a′=gsinα+μgcosα=7.5m/s2
由 v2=2as 得
s2=
=
m
所以最大位移S=s1+s2=
m．
答：小球沿杆运动离出发点的最远距离是
m．
解：（1）对小球受力分析如图，则有：Fsinα-f-mgsinα=ma
FN+mgcosα=Fcosα
F=μFN
联立三式解得a=2.5m/s2
答：小球的加速度的大小为a=2.5m/s2．
（2）2s内物体的位移
s1=
| 1 |
| 2 |
2s末物体的速度
v=at=5m/s
撤去力F后，物体受力如图所示，则有
μmgcosα+mgsinα=ma′
a′=gsinα+μgcosα=7.5m/s2
由 v2=2as 得
s2=
| v2 |
| 2a′ |
| 5 |
| 3 |
所以最大位移S=s1+s2=
| 20 |
| 3 |
答：小球沿杆运动离出发点的最远距离是
| 20 |
| 3 |
点评：解决本题的关键正确地进行受力分析，以及知道加速度是联系力学和运动学的桥梁，通过加速度，可以根据力求运动，也可以根据运动求力．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
（2009?宜昌模拟）在如图所示的电路中，当滑动变阻器的滑片向b端移动时（ ）
（2009?宜昌模拟）如图所示，晾晒衣服的绳子轻且光滑，悬挂衣服的衣架的挂钩也是光滑的，轻绳两端分别固定在两根竖直杆上的A、B两点，衣服处于静止状态．如果保持绳子A端位置不变，将B端分别移动到不同的位置．下列判断正确的（ ）
（2009?宜昌模拟）如图所示，虚线a、b、c是电场中的三个等势面，相邻等势面间的电势差相同，实线为一个带正电的质点仅在电场力作用下，通过该区域的运动轨迹，P、Q是轨迹上的两点．下列说法中正确的是（ ）