题目内容
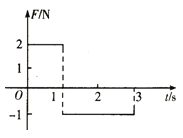
【题目】如图甲所示的电路中,R1、R2均为定值电阻,且R1=100 Ω,R2阻值未知,R3为一滑动变阻器,当其滑片P从左端滑至右端时,测得电源的路端电压随电源中流过的电流变化图线如图乙所示,其中A、B两点是滑片P在变阻器的两个不同端点得到的,求:

(1)电源的电动势和内阻;
(2)定值电阻R2的阻值;
(3)滑动变阻器的最大阻值
【答案】(1)20 Ω (2)5 Ω (3)300 Ω
【解析】试题分析:电源的路端电压随电流的变化图线斜率大小等于电源的内阻,由闭合电路欧姆定律求出电动势;当滑片滑到最右端时,R1被短路,外电路的电阻最小,电流最大,读出电流和电压,由欧姆定律求出R2的阻值;滑动变阻器阻值最大时,外电阻最大,电流最小,由图读出电压和电流,由欧姆定律求出滑动变阻器的最大阻值。
(1)由闭合电路欧姆定律得E=U+Ir,将图象中A、B两点的电压和电流代入和得
E=16+0.2r
E=4+0.8r
联立解得 E=20V r=20Ω。
(2)当R3的滑键自左向右滑时,R3阻值变小,使电路总电阻变小,而总电流变大.由此可知,图线上的A、B两点是滑键分别位于最左端和最右端时所得到的.当滑键位于最右端时,R3=0,R1被短路,外电路总电阻即为R2,故由B点的U、I值可求出R2,![]() 。
。
(3)当滑键在最左端时,其阻值最大,并对应着图线上的A点,故由A点的U、I值可求出此时外电路总电阻,再根据串、并联电路的规律可求出R3的最大值.![]() ,
,
又有 ![]() ,代入数值解得滑动变阻器的最大值R3=300Ω。
,代入数值解得滑动变阻器的最大值R3=300Ω。

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】拥堵已成为现代都市一大通病,发展“空中轨道列车”(简称空轨)是缓解交通压力重要举措.如图所示,它是一种悬挂式单轨交通系统,不仅施工简单、快捷,造价也仅为地铁造价的六分之一左右,下表是有关空轨列车的部分参数.假如多辆空轨列车在同一轨道上同向行驶,为了安全,前后车之间应保持必要的距离,假设前方车辆突然停止,后车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s,求空轨列车的安全车距应至少设定为多少?(g=10m/s2)
行车速度 | 约13m/s | 车辆起动加速度 | 1.0m/s2 |
车辆高度 | 2623mm | 紧急制动加速度 | 6.50m/s2 |
车辆宽度 | 2244mm | 车辆净重 | 8455kg |
平面转弯半径 | ≥30m | 车辆满载重 | 15000kg |