题目内容
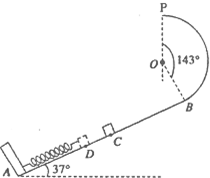 如图所示,AB为倾角θ=37°的斜面轨道,轨道的AC部分光滑,CB部分粗糙.BP为圆心角等于143°半径R=1m的竖直光滑圆弧形轨道,两轨道相切于B点,P、0两点在同一竖茛线上,轻弹簧一端固定在A点,另一 0由端在斜面上C点处,现有一质量m=2kg的物块在外力作用下将弹簧缓慢压缩到D点后(不栓接)释放,物块经过C点后,从C点运动到B点过程中的位移与时间的关系为x=12t-4t2(式中X单位是m,t单位是s),假设物块笫一次经过B点后恰能到达P点,sin37°=0.6,cos37°=0.8,g取1Om/s2.
如图所示,AB为倾角θ=37°的斜面轨道,轨道的AC部分光滑,CB部分粗糙.BP为圆心角等于143°半径R=1m的竖直光滑圆弧形轨道,两轨道相切于B点,P、0两点在同一竖茛线上,轻弹簧一端固定在A点,另一 0由端在斜面上C点处,现有一质量m=2kg的物块在外力作用下将弹簧缓慢压缩到D点后(不栓接)释放,物块经过C点后,从C点运动到B点过程中的位移与时间的关系为x=12t-4t2(式中X单位是m,t单位是s),假设物块笫一次经过B点后恰能到达P点,sin37°=0.6,cos37°=0.8,g取1Om/s2.试求:
(1)若
. | CD |
(2)B、C两点间的距离x
(3)若在P处安装一个竖直弹性挡板,小物块与挡板碰撞时间极短且无机械能损火,小物块与弹簧相互作用不损失机械能,试通过计箅判断物块在第一次与挡板碰撞后的运动过程中是否会脱离轨道?
分析:(1)物体在CB段向上做匀减速直线运动,根据位移与时间的关系得出C点的速度,然后对DC段运用动能定理,求出弹力所做的功.
(2)根据CB段匀减速直线运动的位移时间关系得出物体运动的加速度,从而根据牛顿第二定律求出动摩擦因数,因为物体恰好到达P点,根据牛顿第二定律得出P点的速度,通过机械能守恒定律得出B点的速度,然后通过匀变速直线运动的速度位移公式求出B、C两点间的距离x.
(3)根据动能定理判断物体能否返回时回到与O点等高的位置,若不能回到等高的位置,则小球将不会脱离轨道.
(2)根据CB段匀减速直线运动的位移时间关系得出物体运动的加速度,从而根据牛顿第二定律求出动摩擦因数,因为物体恰好到达P点,根据牛顿第二定律得出P点的速度,通过机械能守恒定律得出B点的速度,然后通过匀变速直线运动的速度位移公式求出B、C两点间的距离x.
(3)根据动能定理判断物体能否返回时回到与O点等高的位置,若不能回到等高的位置,则小球将不会脱离轨道.
解答:解:(1)由,x=12t-4t2知,物块在C点速度为v0=12m/s.
设物块从D点运动到C点的过程中,弹簧对物块所做的功为W,由动能定理得:
W-mgsin37°?
=
mv02
代入数据得:W=
mv02+mgsin37°?
=156J.
(2)由x=12t-4t2知,物块从C运动到B过程中的加速度大小为a=8m/s2.
设物块与斜面间的动摩擦因数为μ,由牛顿第二定律得
mgsinθ+μmgcosθ=ma 代入数据解得
μ=0.25.
物块在P点的速度满足mg=m
.
物块从B运动到P的过程中机械能守恒,则有
物块从C运动到B的过程中有 vB2-v02=-2ax.
由以上各式解得x=
m.
(3)假设物块第一次从圆弧轨道返回并与弹簧相互作用后,能够回到与O点等高的位置Q点,且设其速度为vQ,由动能定理得
mvQ2-
mvp2=mgR-2μmgxcos37°
解得vQ2=-19<0
可见物块返回后不能到达Q点,故物块在以后的运动过程中不会脱离轨道.
答:(1)弹簧对物块所做的功为156J.
(2)B、C两点间的距离x为
m.
(3)物块在以后的运动过程中不会脱离轨道.
设物块从D点运动到C点的过程中,弹簧对物块所做的功为W,由动能定理得:
W-mgsin37°?
. |
| CD |
| 1 |
| 2 |
代入数据得:W=
| 1 |
| 2 |
. |
| CD |
(2)由x=12t-4t2知,物块从C运动到B过程中的加速度大小为a=8m/s2.
设物块与斜面间的动摩擦因数为μ,由牛顿第二定律得
mgsinθ+μmgcosθ=ma 代入数据解得
μ=0.25.
物块在P点的速度满足mg=m
| vp2 |
| R |
物块从B运动到P的过程中机械能守恒,则有
物块从C运动到B的过程中有 vB2-v02=-2ax.
由以上各式解得x=
| 49 |
| 8 |
(3)假设物块第一次从圆弧轨道返回并与弹簧相互作用后,能够回到与O点等高的位置Q点,且设其速度为vQ,由动能定理得
| 1 |
| 2 |
| 1 |
| 2 |
解得vQ2=-19<0
可见物块返回后不能到达Q点,故物块在以后的运动过程中不会脱离轨道.
答:(1)弹簧对物块所做的功为156J.
(2)B、C两点间的距离x为
| 49 |
| 8 |
(3)物块在以后的运动过程中不会脱离轨道.
点评:本题综合考查了动能定理、机械能守恒定律以及牛顿第二定律,对学生的能力要求较高,关键理清物体的运动情况,选择合适的规律进行求解.

练习册系列答案
相关题目
 物理学中有些问题的结论不一定必须通过计算才能验证,有时只需要通过一定的分析就可以判断结论是否正确.如图所示,AB为倾角为θ的斜面,小球从A点以初速度v0(方向与斜面成α角)抛出,恰好落到斜面底端的B点,不计空气阻力,则AB两点间的距离为( )
物理学中有些问题的结论不一定必须通过计算才能验证,有时只需要通过一定的分析就可以判断结论是否正确.如图所示,AB为倾角为θ的斜面,小球从A点以初速度v0(方向与斜面成α角)抛出,恰好落到斜面底端的B点,不计空气阻力,则AB两点间的距离为( ) (式中x单位是m , t单位是s),假设物块笫一次经过B点后恰能到达P点,(sin 37°=0.6,cos 37°=0.8),g取1Om/s2。
(式中x单位是m , t单位是s),假设物块笫一次经过B点后恰能到达P点,(sin 37°=0.6,cos 37°=0.8),g取1Om/s2。

