题目内容
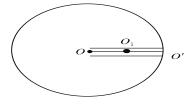
【题目】在水平圆盘上有一过圆心的光滑水平槽,槽内有两根原长、劲度系数均相同的橡皮绳拉住一质量为m的小球,一条橡皮绳拴在O点,另一条拴在O′点,球在O1点, O点为圆盘的中心,O′点为圆盘的边缘.橡皮绳的劲度系数为k,原长为圆盘半径R的![]() ,现使圆盘角速度由零缓慢增大,求
,现使圆盘角速度由零缓慢增大,求
(1) 当橡皮绳OO1拉伸而O1O′刚好为原长时,圆盘的角速度?
(2) 圆盘的角速度为ω2=![]() 时,小球圆周运动的半径R2?
时,小球圆周运动的半径R2?
(3) 圆盘的角速度为ω1=![]() 时,小球圆周运动的半径R1?
时,小球圆周运动的半径R1?
【答案】(1)![]() (2)
(2) ![]() (3)
(3)![]()
【解析】
(1) 当橡皮绳OO1拉伸而O1O′刚好为原长时,设小球做匀速圆周运动的角速度为ω0,由牛顿第二定律有:![]()
解得:![]()
(2)当![]() 时,此时橡皮绳O1O′松弛,则有:
时,此时橡皮绳O1O′松弛,则有:![]()
解得:![]()
(3)当![]() 时,橡皮绳OO1和橡皮绳O1O′都是拉伸的,则有:
时,橡皮绳OO1和橡皮绳O1O′都是拉伸的,则有:
![]()
解得:![]()

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目