题目内容
11. 我国的“天链一号”星是地球同步轨道卫星,可为载人航天器及中低轨道卫星提供数据通讯.如图为“天链一号“星a、赤道平面内的低轨道卫星 b、地球的位置关系示意图,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍.已知卫星a、b绕地球同向运行,卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入与卫星 a通讯的盲区.卫星间的通讯信号视为沿直线传播,信号传输时间可忽略.下列分析正确的是( )
我国的“天链一号”星是地球同步轨道卫星,可为载人航天器及中低轨道卫星提供数据通讯.如图为“天链一号“星a、赤道平面内的低轨道卫星 b、地球的位置关系示意图,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍.已知卫星a、b绕地球同向运行,卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入与卫星 a通讯的盲区.卫星间的通讯信号视为沿直线传播,信号传输时间可忽略.下列分析正确的是( )| A. | 张角θ1和θ2满足sinθ2=4sinθ1 | |
| B. | 卫星b星的周期为$\frac{T}{4}$ | |
| C. | 卫星b每次在盲区运行的时间为$\frac{{θ}_{1}+{θ}_{2}}{14π}$T | |
| D. | 卫星b每次在盲区运行的时间为$\frac{{θ}_{1}+{θ}_{2}}{16π}$T |
分析 根据几何关系求解张角θ1和θ2满足的关系,由万有引力提供向心力,列式求解卫星b的周期.卫星间的通讯信号视为沿直线传播,由几何关系得到卫星b在盲区有两个边缘相对于地球的张角,再求解在盲区运行的时间.
解答 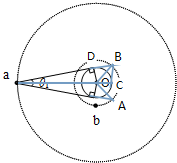 解:A、设卫星a、b的轨道半径分别为r1和r2.地球半径为R.
解:A、设卫星a、b的轨道半径分别为r1和r2.地球半径为R.
由几何知识得:tan$\frac{{θ}_{1}}{2}=\frac{R}{{r}_{1}}$,tan$\frac{{θ}_{2}}{2}=\frac{R}{{r}_{2}}$
由题 r1=4r2.则得 4tan$\frac{{θ}_{1}}{2}$=tan$\frac{{θ}_{2}}{2}$,由数学知识sinθ2≠4sinθ1.故A错误.
B、由$\frac{GMm}{{{r}_{\;}}^{2}}=m\frac{4{π}^{2}}{{{T}_{\;}}^{2}}$r
可得 T=2$π\sqrt{\frac{{r}^{3}}{GM}}$,可得 r1=4r2.则得卫星b星的周期为$\frac{T}{8}$,故B错误.
CD、如图,A、B是卫星盲区两个边缘位置,由几何知识可得∠AOB=θ1+θ2,则 ($\frac{\frac{2π}{T}}{8}-\frac{2π}{T}$)t=∠AOB=θ1+θ2,
解得,b每次在盲区运行的时间为 t=$\frac{{θ}_{1}+{θ}_{2}}{14π}$T,故C正确,D错误.
故选:C
点评 本题既要掌握卫星问题的基本思路:万有引力提供向心力,更重要的是画出示意图,运用几何知识解答.

练习册系列答案
相关题目
1.有一电阻极小的导线绕制而成的线圈接在交流电源上,如果电源电压的峰值保持一定,下边哪种情况下,能使通过线圈的电流减小( )
| A. | 减小电源的频率 | |
| B. | 增大电源的频率 | |
| C. | 保持电源的频率不变,在线圈中加入铁芯 | |
| D. | 保持电源的频率不变,减少线圈的匝数 |
2.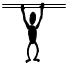 某同学在做引体向上时,两臂伸直对称吊在单杠上,两臂夹角为60°,已知该同学的体重为60kg,则两只手臂的拉力分别是( )(g取10m/s2)
某同学在做引体向上时,两臂伸直对称吊在单杠上,两臂夹角为60°,已知该同学的体重为60kg,则两只手臂的拉力分别是( )(g取10m/s2)
 某同学在做引体向上时,两臂伸直对称吊在单杠上,两臂夹角为60°,已知该同学的体重为60kg,则两只手臂的拉力分别是( )(g取10m/s2)
某同学在做引体向上时,两臂伸直对称吊在单杠上,两臂夹角为60°,已知该同学的体重为60kg,则两只手臂的拉力分别是( )(g取10m/s2)| A. | 300N | B. | 200$\sqrt{3}$N | C. | 100N | D. | 600N |
6.压敏电阻的阻值随所受压力的增大而减小,有位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图1所示,将压敏电阻及各电路元件和一块挡板固定在绝缘小车上,中间放置一个光滑的绝缘重球.已知0到t1时间内小车静止,重球对压敏电阻和挡板均无压力.此后小车向右做直线运动,整个过程中,电流表示数随时间的变化图线如图2所示,则下列判断正确的是( )


| A. | 从t1到t2时间内,小车做匀速直线运动 | |
| B. | 从t2到t3时间内,小车做匀加速直线运动 | |
| C. | 从t3到t4时间内,小车做匀加速直线运动 | |
| D. | 从t4到t5时间内,小车一定处于静止状态 |
16. 今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U.,电阻恒为R)恰能正常发光,则( )
今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U.,电阻恒为R)恰能正常发光,则( )
 今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U.,电阻恒为R)恰能正常发光,则( )
今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U.,电阻恒为R)恰能正常发光,则( )| A. | 变压器的匝数比为U0:U | |
| B. | 电流表的示数为$\frac{{{U}_{0}}^{2}}{RU}$ | |
| C. | 在图示位置时,发电机线圈的磁通量为$\frac{{\sqrt{2}U}}{2Nnπ}$ | |
| D. | 从图示位置开始计时,变压器输入电压的瞬时值表达式为u=Usin2nπt |
3.物体做匀加速直线运动,已知加速度为5m/s2,那么在任意1s内( )
| A. | 物体的末速度一定等于初速度的5倍 | |
| B. | 物体的末速度一定比初速度大5m/s | |
| C. | 物体的初速度一定比前1s内的末速度大5m/s | |
| D. | 物体的末速度一定比前1s内的初速度大5m/s |
20.在下列各种措施中,利用静电作用的是( )
| A. | 电视机后盖上开有许多小孔 | B. | 静电除尘 | ||
| C. | 静电喷涂 | D. | 静电复印 |
 如图所示,上端开口的足够长光滑圆形气缸竖直装置,截面积为40cm2的活塞将一定质量的气体封闭在气缸内.在气缸内距缸底60cm处设有薄卡环ab,使活塞只能向上滑动.开始时活塞搁在ab上,缸内气体的压强等于大气压强p0=1.0×105 Pa,温度为300K.现缓慢加热汽缸内气体,当温度缓慢升高到330K,活塞恰好离开ab.(g取10m/s2)求:
如图所示,上端开口的足够长光滑圆形气缸竖直装置,截面积为40cm2的活塞将一定质量的气体封闭在气缸内.在气缸内距缸底60cm处设有薄卡环ab,使活塞只能向上滑动.开始时活塞搁在ab上,缸内气体的压强等于大气压强p0=1.0×105 Pa,温度为300K.现缓慢加热汽缸内气体,当温度缓慢升高到330K,活塞恰好离开ab.(g取10m/s2)求: