Question

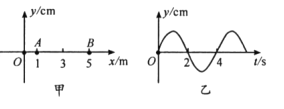
【题目】如图甲所示，一只蚂蚁在倾角为θ=37°的大理石斜面上沿直线向上拖拉质量为m＝1g的食物。t＝0时刻从A点出发，若蚂蚁对食物拖拉的作用力F可以简化成按如图乙所示规律变化；第3 s末运动到B点时速度刚好为0，此时蚂蚁松开食物，食物下滑，第4s末食物刚好回到A点。已知食物与大理石面间的动摩擦因数μ＝0.7，sin37°=0.6，cos37°=0.8 (食物可视为质点，空气阻力忽略不计)。求：

(1) A、B间的距离及返回A点时速度的大小；

(2) 若蚂蚁沿斜面向上拖拉食物时，食物对斜面的压力大小恒为3×10-3N，则拖拉过程拖拉力F的平均功率是多少?

(3) 若在 A 点恰好有另外一只蚂蚁，遇到该下滑的食物时，立即施加给食物沿斜面向上的大小为1×10-3N的恒力，则食物在距离A点多远处方才停下？（忽略接触瞬间的碰撞影响，斜面足够长）

Answer 1

【答案】（1） （2） (3)

【解析】

(1)由牛顿第二定律有，下滑的加速度为：

上拖过程AB的位移大小为：

下落到A点的速度为：

；

(2)由动能定理有：

拖拉力F的平均功率为：

；

(3)食物受到的合外力

又

解得：。