题目内容
一位蹦床运动员仅在竖直方向上运动,弹簧床对运动员的弹力F随时间t的变化规律通过传感器用计算机绘制出来,如图所示.结合图象,g=10m/s2,试求: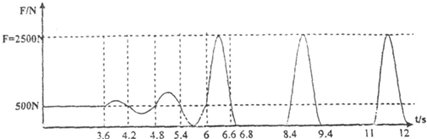
(1)运动员的质量;
(2)不计空气阻力,运动过程中,运动员最大加速度;
(3)不计空气阻力,运动过程中,运动员离开蹦床上升的最大高度.

(1)运动员的质量;
(2)不计空气阻力,运动过程中,运动员最大加速度;
(3)不计空气阻力,运动过程中,运动员离开蹦床上升的最大高度.
分析:(1)根据运动员停止在蹦床上时,根据重力和压力相等求出质量的大小.
(2)结合最大弹力,运用牛顿第二定律求出运动员的最大加速度.
(3)根据图线得出运动员在空中的时间,因为运动员在空中做竖直上抛运动,上升和下降的时间相等,结合下降的时间,通过位移公式求出最大高度.
(2)结合最大弹力,运用牛顿第二定律求出运动员的最大加速度.
(3)根据图线得出运动员在空中的时间,因为运动员在空中做竖直上抛运动,上升和下降的时间相等,结合下降的时间,通过位移公式求出最大高度.
解答:解:(1)曲线一开始是运动员停在蹦床上,压力是500N.于是运动员重力是500N.
则运动员质量为:m=
=
=50Kg.
(2)最大弹力:Fm=2500N,
根据牛顿第二定律得:Fm-mg=mam
代入数据解得:am=40m/s2.
(3)运动员在空中时间:t0=8.4-6.8s=1.6s
下落时间:t=
=0.8s,
最大高度:h=
gt2=
×10×0.64m=3.2m.
答:(1)运动员的质量为50kg.
(2)运动员的最大加速度为40m/s2.
(3)运动员离开蹦床上升的最大高度为3.2m.
则运动员质量为:m=
| F |
| g |
| 500 |
| 10 |
(2)最大弹力:Fm=2500N,
根据牛顿第二定律得:Fm-mg=mam
代入数据解得:am=40m/s2.
(3)运动员在空中时间:t0=8.4-6.8s=1.6s
下落时间:t=
| t0 |
| 2 |
最大高度:h=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)运动员的质量为50kg.
(2)运动员的最大加速度为40m/s2.
(3)运动员离开蹦床上升的最大高度为3.2m.
点评:本题考查了牛顿第二定律和图象的综合,关键知道人静止时,重力等于弹力,弹力最大时,加速度最大,弹力为零时,人在空中.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 一位蹦床运动员仅在竖直方向上运动.弹簧对运动员的弹力F随时间t的变化规律通过一传感器用计算机绘制出来,如图所示,取重力加速度g=10m/s2(不计阻力),试根据图象提供的信息,求:
一位蹦床运动员仅在竖直方向上运动.弹簧对运动员的弹力F随时间t的变化规律通过一传感器用计算机绘制出来,如图所示,取重力加速度g=10m/s2(不计阻力),试根据图象提供的信息,求:


