题目内容
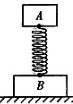
如右图所示，轻弹簧下面挂一质量为m的小钢球，小球在竖直方向上做振幅为A的简谐运动（空气阻力忽略不计），当小球振动到最高点时，弹簧正好为原长．则小球在振动过程中（ ）分析：A、根据机械能守恒的条件小球是否机械能守恒；
B、根据最高点和最高点关于平衡位置对称得到小球最低点的合力然后根据牛顿第二定律求加速度；
C、在最低点弹性势能最大，根据能量守恒定律，求出最低点的弹性势能．
D、回复力指小球受到的合力，可以根据动量定理计算．
B、根据最高点和最高点关于平衡位置对称得到小球最低点的合力然后根据牛顿第二定律求加速度；
C、在最低点弹性势能最大，根据能量守恒定律，求出最低点的弹性势能．
D、回复力指小球受到的合力，可以根据动量定理计算．
解答：解：A、除了小球重力外还有弹簧弹力做功，故小球机械能不守恒，弹簧和小球组成的系统机械能守恒，所以A错误
B、小球做简谐运动的平衡位置处，mg=kx，x=
．当物体振动到最高点时，弹簧正好为原长，可知x=A．所以在最低点时，形变量为2A．弹力大小为2mg．则小球所受合力为2mg-mg=mg根据牛顿第二定律得小球加速度大小等于g，故B正确．
C、从最高点到最低点，动能变化为0，重力势能减小2mgA，则弹性势能增加2mgA．而初位置弹性势能为0，在最低点弹性势能最大，为2mgA．故C正确．
D、从最高点到平衡位置回复力向下，冲量向下，从平衡位置到最低点回复力向上，则冲量向上，故回复力的总冲量为0．所以D错误．
故选BC．
B、小球做简谐运动的平衡位置处，mg=kx，x=
| mg |
| k |
C、从最高点到最低点，动能变化为0，重力势能减小2mgA，则弹性势能增加2mgA．而初位置弹性势能为0，在最低点弹性势能最大，为2mgA．故C正确．
D、从最高点到平衡位置回复力向下，冲量向下，从平衡位置到最低点回复力向上，则冲量向上，故回复力的总冲量为0．所以D错误．
故选BC．
点评：解决本题的关键抓住简谐运动的对称性以及灵活运用能量守恒定律和机械能守恒定律．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
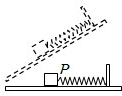如图所示，轻弹簧的一端与物块P相连，另一端固定在木板上．先将木板水平放置，并使弹簧处于拉伸状态．缓慢抬起木板的右端，使倾角逐渐增大，直至物块P刚要沿木板向下滑动，在这个过程中，物块P所受静摩擦力的大小变化情况是（ ）
如右图所示，物体a、b用一根不可伸长的细线相连，再用一根轻弹簧跟a相连，弹簧上端固定在天花板上，已知物体a、b的质量相等，系统处于静止状态．当P点处绳子剪断的瞬间（ ）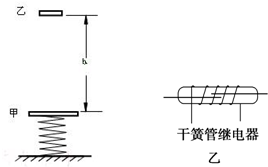
质量m=1.0kg的甲物体与竖直放置的轻弹簧的上端连接，弹簧下端固定在地面上，如右图所示．质量m=1.0kg的乙物体从甲物体正上方，距离甲物体h=0.40m处自由落下，撞在甲物体上在极短的时间内与甲物体粘在一起（不再分离）向下运动．它们到达最低点后又向上运动，上升的最高点比甲物体初始位置高H=0.10m．已知弹簧的劲度系数k=200N/m，且弹簧始终在弹性限度内，空气阻力可忽略不计，重力加速度g取10m/s2．求：
