��Ŀ����
�����ۡ��ߺŷɴ���2008��9��25����9ʱ10�ִӾ�Ȫ���Ƿ������ķ������գ��ɴ���̫��Ԥ������Ƶ����������ʮ��Ȧ�������ڼ䣬����Ա���г����ڵ�����ָ֯�ӺͲ��ϵͳ��Эͬ����£�˳������˿ռ���ջ��һϵ�пռ��ѧ���飮28��17ʱ37�֣������ۡ��ߺŷɴ������ɹ��в�Ԥ������ɹ���½�����ִ�з�������ĺ���Ա��־�ա��������;�������ȫ���գ��й������ߺ����˺�����л��Բ���ɹ����ɴ����պ���������Բ������У����ص�ԼΪ200���Զ�ص�ԼΪ347������Ƶ������5Ȧ���淢��ָ�ʹ�ɴ��ϵķ������ڷɴ�����Զ�ص�ʱ�Զ����ʵ�б�죬����˷ɴ����ٶȣ�ʹ�÷ɴ��ھ����343�����Բ����Ϸ��У��������뾶ΪR��������������ٶ�Ϊg ��
��1���Է�������Ա�ڲ��ڡ�Ư�������������������ԭ��
��2���������ߺš��ɴ����Ƶط���5Ȧ����б�죬��ԭ������Բ�����Ϊ������Ϊh ��Բ�ι������ɴ�������Բ�ι�����е������Ƕ��٣�����h��R��g��ʾ��
��3�����ز��ڽ�Ҫ��½֮ǰ�����ڿ�������������һ������������̣��������������ٶȵ�ƽ�������ȣ�����ϵ��Ϊk�����زյ�����Ϊm���������½����̵��������ٶ�Ϊ����˹����з��زյ��ٶȣ��Լ������½������е�λʱ����ת��Ϊ���ܵĻ�е��Ϊ���٣�
��1���Է�������Ա�ڲ��ڡ�Ư�������������������ԭ��
��2���������ߺš��ɴ����Ƶط���5Ȧ����б�죬��ԭ������Բ�����Ϊ������Ϊh ��Բ�ι������ɴ�������Բ�ι�����е������Ƕ��٣�����h��R��g��ʾ��
��3�����ز��ڽ�Ҫ��½֮ǰ�����ڿ�������������һ������������̣��������������ٶȵ�ƽ�������ȣ�����ϵ��Ϊk�����زյ�����Ϊm���������½����̵��������ٶ�Ϊ����˹����з��زյ��ٶȣ��Լ������½������е�λʱ����ת��Ϊ���ܵĻ�е��Ϊ���٣�
��������1���Ա���ܵ����������ȫ���ṩ�Ƶ�����Բ���˶���������������Ա������ȫʧ��״̬��
��2�������������ṩ���������г����ڱ���ʽ�������ûƽ������GM���������������ڱ���ʽ
��3�������˶�ʱ�������ڿ����������ɴ˿��Եõ������˶����ٶȣ�����������������ת��Ϊ���ڵĻ�е�ܣ�������������½������е�λʱ����ת��Ϊ���ܵĻ�е�ܣ�
��2�������������ṩ���������г����ڱ���ʽ�������ûƽ������GM���������������ڱ���ʽ
��3�������˶�ʱ�������ڿ����������ɴ˿��Եõ������˶����ٶȣ�����������������ת��Ϊ���ڵĻ�е�ܣ�������������½������е�λʱ����ת��Ϊ���ܵĻ�е�ܣ�
����⣺��1���Ա���ܵ����������ȫ���ṩ�Ƶ�����Բ���˶���������������Ա������ȫʧ��״̬��
��2���ɴ��Ƶ���������Բ���˶������������ṩ�����������У�
G
=m(R+h)
��
�ر�������������������ܵ����������������У�
m��g=G
��
��ã�
GM=gR2
�����ʽ�ã�
=(R+h)
��ã�
T=
��3�������������Ϊf���������֪ f=kv2�������½�ʱ��f=mg�䣬��kv2=mg��
�ɴ˿ɽ�������½����ٶ�Ϊ��v=
��
������������ʱ��е��ת��Ϊ���ܣ��ʵ�λʱ����ת��Ϊ���ܵĻ�е��Ϊ��
W=fvt=kv3=
��
��1���Ա���ܵ����������ȫ���ṩ�Ƶ�����Բ���˶���������������Ա������ȫʧ��״̬��
��2������ΪT=
��3���˹����з��زյ��ٶ�Ϊv=
�����½������е�λʱ����ת��Ϊ���ܵĻ�е��Ϊ
��2���ɴ��Ƶ���������Բ���˶������������ṩ�����������У�
G
| Mm |
| (R+h)2 |
| 4��2 |
| T2 |
�ر�������������������ܵ����������������У�
m��g=G
| Mm�� |
| R2 |
��ã�
GM=gR2
�����ʽ�ã�
| gR2 |
| (R+h)2 |
| 4��2 |
| T2 |
��ã�
T=
| 2��(R+h) |
| R |
|
��3�������������Ϊf���������֪ f=kv2�������½�ʱ��f=mg�䣬��kv2=mg��
�ɴ˿ɽ�������½����ٶ�Ϊ��v=
| mg�� |
| k |
������������ʱ��е��ת��Ϊ���ܣ��ʵ�λʱ����ת��Ϊ���ܵĻ�е��Ϊ��
W=fvt=kv3=
| m3g��3 |
| k2 |
��
��1���Ա���ܵ����������ȫ���ṩ�Ƶ�����Բ���˶���������������Ա������ȫʧ��״̬��
��2������ΪT=
| 2��(R+h) |
| R |
|
��3���˹����з��زյ��ٶ�Ϊv=
| mg�� |
| k |
�����½������е�λʱ����ת��Ϊ���ܵĻ�е��Ϊ
| m3g��3 |
| k2 |
�����������ص��ڵ������ˣ�����֪��������������ʱ��е��ת��Ϊ���ܣ�����֮�ⶼ�Ǽ�Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
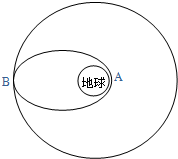 2008��9��25��21ʱ10�֣������ߺŷɴ��ɹ����䣬������2��20Сʱ27���ӣ��Ƶ������45Ȧ����9��28��17ʱ37�ְ�ȫ��½������Ա��־���š����족���⺽�������������������£��ɹ�����˿ռ���ջ��������̫�����ߣ����ջ�������ͷ��˰�����ǣ���Χ�ƹ���ս��а��ʵ�飮�����ߺ����ɳ���-2F���ػ������������ص�ΪA��Զ�ص�ΪB����Բ����ϣ�ʵʩ������Ԥ��Բ��������ģ������ͼ12��ʾ��������ص�A�����߶�Ϊh���ɴ���Ԥ��Բ����Ϸ���nȦ���õ�ʱ��Ϊt�����������������ٶ�Ϊg������뾶R������
2008��9��25��21ʱ10�֣������ߺŷɴ��ɹ����䣬������2��20Сʱ27���ӣ��Ƶ������45Ȧ����9��28��17ʱ37�ְ�ȫ��½������Ա��־���š����족���⺽�������������������£��ɹ�����˿ռ���ջ��������̫�����ߣ����ջ�������ͷ��˰�����ǣ���Χ�ƹ���ս��а��ʵ�飮�����ߺ����ɳ���-2F���ػ������������ص�ΪA��Զ�ص�ΪB����Բ����ϣ�ʵʩ������Ԥ��Բ��������ģ������ͼ12��ʾ��������ص�A�����߶�Ϊh���ɴ���Ԥ��Բ����Ϸ���nȦ���õ�ʱ��Ϊt�����������������ٶ�Ϊg������뾶R������