题目内容
质量为 M、半径为 R 的匀质水平圆盘静止在水平地面上,盘与地面间无摩擦。圆盘中心处有一只质量为 m 的小青蛙(可处理成质点),小青蛙将从静止跳出圆盘。为解答表述一致,将青蛙跳起后瞬间相对地面的水平分速度记为 vx,竖直向上的分速度记为 vy,合成的初始速度大小记为 v,将圆盘后退的速度记为 u。
(1)设青蛙跳起后落地点在落地时的圆盘外。
(1.1)对给定的 vx,可取不同的 vy,试导出跳起过程中青蛙所做功 W 的取值范围,答案中可包含的参量为 M、R、m、g(重力加速度)和 vx。
(1.2)将(1.1)问所得 W 取值范围的下限记为 W0,不同的 vx对应不同的 W0值,试导出其中最小者 Wmin,答案中可包含的参量为 M、R、m 和 g。
(2)如果在原圆盘边紧挨着放另外一个相同的静止空圆盘,青蛙从原圆盘中心跳起后瞬间,相对地面速度的方向与水平方向夹角为 45°,青蛙跳起后恰好能落在空圆盘的中心。跳起过程中青蛙所作功记为 W’,试求 W’与(1.2)问所得 Wmin间的比值 γ=W‘/Wmin,答案中可包含的参量为 M 和 m。
解析:(1) 青蛙跳起后落地点在圆盘外。
(1.1) 青蛙跳起过程,水平方向动量守恒。由动量守恒定律,m vx =M u,
vx t+ut>R,
vy =gt/2,
v2= vx2+ vy2。
跳起过程中青蛙做功 W =![]() m v2+
m v2+![]() Mu2。
Mu2。
联立解得:W >![]() m vx2+
m vx2+![]() +
+![]() .
.
(1.2) W0 =![]() m vx2+
m vx2+![]() +
+![]() =
=![]() +
+![]()
由于![]() ·
·![]() =
=![]() 为定值,根据两个正数积一定,两数相等时,和最小,即
为定值,根据两个正数积一定,两数相等时,和最小,即![]() =
=![]() ,解得vx2=
,解得vx2=![]()
![]() 。
。
可得Wmin =![]()
![]() +
+![]()
![]() .。
.。
(2) 设青蛙起跳速度为v,青蛙跳起过程,水平方向动量守恒。由动量守恒定律,
m vcos 45°=M u,
v cos 45°t=2R,
vsin45°=gt/2,
跳起过程中青蛙做功 W’=![]() m v2+
m v2+![]() Mu2。
Mu2。
联立解得:W ‘=(1+![]() )mgR。
)mgR。
γ=W‘/Wmin =![]()
![]() ..
..
【点评】此题以小青蛙在水平圆盘跳跃切入,意在考查动量守恒定律、功、运动的合成和分解及其相关知识。此题需要运用数学知识求得功的极小值。

 智慧小复习系列答案
智慧小复习系列答案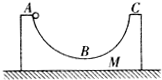 一光滑水平地面上静止放着质量为m、半径为R的光滑圆弧轨道,质量也为m小球从轨道最左端的A点由静止滑下(AC为水平直径),重力加速度为g,下列正确的是( )
一光滑水平地面上静止放着质量为m、半径为R的光滑圆弧轨道,质量也为m小球从轨道最左端的A点由静止滑下(AC为水平直径),重力加速度为g,下列正确的是( )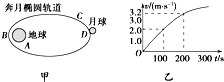 “嫦娥二号”卫星送入近地点高度200公里、远地点高度38万公里的直接奔月轨道,如图14甲所示.卫星奔月飞行约需112小时;当卫星到达月球附近的特定位置时,实施近月制动,进入近月点100公里的椭圆轨道.再经过两次轨道调整,进入100公里的极月圆轨道.
“嫦娥二号”卫星送入近地点高度200公里、远地点高度38万公里的直接奔月轨道,如图14甲所示.卫星奔月飞行约需112小时;当卫星到达月球附近的特定位置时,实施近月制动,进入近月点100公里的椭圆轨道.再经过两次轨道调整,进入100公里的极月圆轨道.