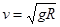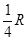题目内容
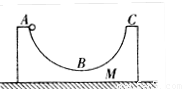
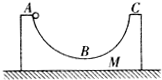 一光滑水平地面上静止放着质量为m、半径为R的光滑圆弧轨道,质量也为m小球从轨道最左端的A点由静止滑下(AC为水平直径),重力加速度为g,下列正确的是( )
一光滑水平地面上静止放着质量为m、半径为R的光滑圆弧轨道,质量也为m小球从轨道最左端的A点由静止滑下(AC为水平直径),重力加速度为g,下列正确的是( )分析:由于水平面光滑,系统水平方向不受外力,水平方向动量守恒.圆弧轨道也光滑,系统的机械能守恒也守恒.根据两大守恒定律进行分析.
解答:解:
A、当小球滑到圆弧的最高点时,根据水平方向动量守恒得知,小球与圆弧的速度均为零,根据系统的机械能守恒得知,小球能滑到右端c.故A错误.
B、设小球通过最低点时小球与轨道的速度分别为v和V,由动量守恒和机械能守恒定律得
mgR=
mv2+
mV2
0=mv+mV
解得,v=
.故B正确.
C、小球向右运动的过程中,轨道先向左加速,后向左减速,当小球到达c点时,速度为零.故C错误.
D、设小球滑到最低点时,轨道向左运动的距离为s,则小球相对于地水平位移大小为:R-s.取水平向右为正方向,
根据系统水平方向动量守恒得:m
-m
=0
解得,s=
所以轨道做往复运动,离原先静止位置最大距离为2s=R.故D错误.
故选B
A、当小球滑到圆弧的最高点时,根据水平方向动量守恒得知,小球与圆弧的速度均为零,根据系统的机械能守恒得知,小球能滑到右端c.故A错误.
B、设小球通过最低点时小球与轨道的速度分别为v和V,由动量守恒和机械能守恒定律得
mgR=
| 1 |
| 2 |
| 1 |
| 2 |
0=mv+mV
解得,v=
| gR |
C、小球向右运动的过程中,轨道先向左加速,后向左减速,当小球到达c点时,速度为零.故C错误.
D、设小球滑到最低点时,轨道向左运动的距离为s,则小球相对于地水平位移大小为:R-s.取水平向右为正方向,
根据系统水平方向动量守恒得:m
| R-s |
| t |
| s |
| t |
解得,s=
| R |
| 2 |
所以轨道做往复运动,离原先静止位置最大距离为2s=R.故D错误.
故选B
点评:本题是系统的水平方向动量守恒和机械能守恒的类型,运用平均动量守恒求解轨道运动的最大距离.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
一光滑水平地面上静止放着质量为m、半径为R的光滑圆弧轨道,质量也为m小球从轨道最左端的A点由静止滑下(AC为水平直径),重力加速度为g,下列正确的是( )
| A.小球不可能滑到圆弧轨道右端最高端c[来源:Z.xx.k.Com] |
B.小球通过最低点时速度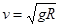 |
| C.小球向右运动中轨道先向左加速运动,后向右加速运动 |
D.轨道做往复运动,离原先静止位置最大距离为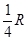 |