题目内容
11.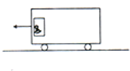 如图所示,货车正在平直公路上以a1=0.2m/s2的加速度启动,同时,一只壁虎从静止开始以a2=0.15 m/s2的加速度在货车壁上向上匀加速爬行.则:
如图所示,货车正在平直公路上以a1=0.2m/s2的加速度启动,同时,一只壁虎从静止开始以a2=0.15 m/s2的加速度在货车壁上向上匀加速爬行.则:(1)2s末,壁虎相对地面的速度大小是多少?
(3)壁虎做直线运动还是曲线运动?(不需要说明原因)
分析 (1)壁虎同时参入了相对于车向上的匀加速运动和随车一起向左的匀加速直线运动.分别求出2s末,两个方向上的速度,根据速度合成原则即可求解;
(2)求出x-y的函数图象,即可分析壁虎的运动情况.
解答 解:(1)壁虎同时参入了相对于车向上的匀加速运动和随车一起向左的匀加速直线运动.经过2s时,壁虎向上运动的速度为:
vy=v2=a2t=0.3m/s,
随车运动的速度为:vx=v1=a1t=0.4m/s,
如图1所示,壁虎运动的合速度在t=2s末,大小为:v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=0.5m/s,
(2)如图2,在汽车启动后2s这段时间内,壁虎做直线运动;
答:(1)经过2s时,地面上的人看到壁虎的速度大小为0.5m/s;
(2)壁虎相对于地面做直线运动.
点评 本题的解题方向与平抛运动相似,把壁虎的运动分解到水平和竖直方向研究,难度适中.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
1.入射光照射到某金属表面上发生光电效应,若入射光强度减弱,而频率不变,则( )
| A. | 有可能不发生光电效应 | |
| B. | 逸出的光电子的最大初动能将减小 | |
| C. | 单位时间内从金属表面逸出的光电子数目将减小 | |
| D. | 从光照至金属表面上到发射出光电子之间的时间间隔将明显增加 |
2.下列关于温度、内能和热量的说法中正确的是( )
| A. | 物体的温度越高,所含热量越多 | |
| B. | 物体的内能越大,所含热量越多 | |
| C. | 物体的温度越高,它的分子热运动的平均动能越大 | |
| D. | 物体的温度不变,它的内能就不变 |
19.高速或超速离心机是基因提取中的关键设备,当超速离心机转速达80000r/min时,则关于距离超速离心机转轴12cm处的质点,下列说法正确的是( )
| A. | 周期为$\frac{1}{80000}$s | B. | 线速度大小为320πm/s | ||
| C. | 角速度为160000πrad/s | D. | 角速度为$\frac{4000}{3}$rad/s |
6. 如图所示,飞船从轨道2变轨至轨道1,若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道2上,飞船在轨道1上的( )
如图所示,飞船从轨道2变轨至轨道1,若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道2上,飞船在轨道1上的( )
 如图所示,飞船从轨道2变轨至轨道1,若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道2上,飞船在轨道1上的( )
如图所示,飞船从轨道2变轨至轨道1,若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道2上,飞船在轨道1上的( )| A. | 速度大 | B. | 向心加速度大 | C. | 运行周期长 | D. | 角速度大 |
16.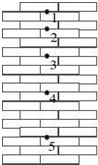 小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )
小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )
 小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )
小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )| A. | 能判定位置“1”是小球释放的初始位置 | |
| B. | 能求出小球下落的加速度大小为a=$\frac{d}{4{T}^{2}}$ | |
| C. | 能求出小球在位置“3”的速度大小为V=$\frac{7d}{T}$ | |
| D. | 如果再知道当地的重力加速度,就可以验证小球下落过程中机械能是否守恒 |
3. 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )
 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )| A. | 此时这两颗卫星的向心加速度一定相等 | |
| B. | 如果使卫星l加速,它就一定能追上卫星2 | |
| C. | 卫星1由位置A运动至位置B所需的时间为$\frac{πr}{3R}\sqrt{\frac{r}{g}}$ | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做正功 |
20.将行星绕太阳的运动看做是匀速圆周运动,若已知万有引力常量G,要求出太阳的质量还需要知道下列哪些数据( )
| A. | 行星绕太阳运动的开普勒常量k | |
| B. | 地球的公转周期,地球表面重力加速度 | |
| C. | 火星质量,火星半径,火星的公转周期 | |
| D. | 金星的公转轨道半径,金星的公转周期 |
1. 已知真空中电荷量为q的静止点电荷,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r处的电势为φ=$\frac{kq}{r}$(k为静电力常量).如图所示,两电荷量为+Q和-q的异种点电荷相距为d,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )
已知真空中电荷量为q的静止点电荷,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r处的电势为φ=$\frac{kq}{r}$(k为静电力常量).如图所示,两电荷量为+Q和-q的异种点电荷相距为d,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )
 已知真空中电荷量为q的静止点电荷,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r处的电势为φ=$\frac{kq}{r}$(k为静电力常量).如图所示,两电荷量为+Q和-q的异种点电荷相距为d,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )
已知真空中电荷量为q的静止点电荷,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r处的电势为φ=$\frac{kq}{r}$(k为静电力常量).如图所示,两电荷量为+Q和-q的异种点电荷相距为d,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )| A. | 增加$\frac{2kQeR}{{{d^2}+{R^2}}}$ | B. | 减少$\frac{2kqeR}{{{d^2}-{R^2}}}$ | ||
| C. | 增加$\frac{2kqeR}{{{d^2}+{R^2}}}$ | D. | 减少$\frac{2kQeR}{{{d^2}-{R^2}}}$ |