题目内容
11．
质量1kg的物体，放在桌面上受到斜向上方的拉力F作用，并沿水平桌面运动，F与水平面的夹角为30°，如图所示，已知F=4N，物体与桌面的滑动摩擦力f=1.6N．求：（1）物体运动的加速度
（2）从静止开始10s内物体前进的路程．
分析 （1）对物体受力分析，受到拉力、重力、支持力和向后的滑动摩擦力，根据受力分析和牛顿第二定律列方程求解加速度；
（2）结合匀变速直线运动的位移公式即可求出．
解答 解：（1）对物体受力分析如图所示：
水平方向：ma=Fcos30°-f
代入数据得：a=1.86m/s2
（2）物体的初速度为0，则10s内的位移：$x=\frac{1}{2}a{t}^{2}=\frac{1}{2}×1.86×1{0}^{2}=93$m
答：（1）物体运动的加速度是1.86m/s2；
（2）从静止开始10s内物体前进的路程是93m．
点评 本题考查牛顿第二定律的一般应用问题，关键是受力分析后，将拉力沿着水平和竖直方向正交分解，然后结合牛顿第二定律列方程求解．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
5．下列公式中定义的物理量不是采用比值定义法得出的是（ ）
| A． | E=$\frac{F}{q}$ | B． | R=ρ$\frac{I}{S}$ | C． | B=$\frac{F}{IL}$ | D． | C=$\frac{Q}{U}$ |
6．
如图所示，小球P、Q的质量相等，其间用轻弹簧相连，光滑斜面倾角为θ，系统静止时，弹簧与轻绳均平行与斜面，则在轻绳被突然剪断的瞬间，下列说法不正确的是（ ）
如图所示，小球P、Q的质量相等，其间用轻弹簧相连，光滑斜面倾角为θ，系统静止时，弹簧与轻绳均平行与斜面，则在轻绳被突然剪断的瞬间，下列说法不正确的是（ ）| A． | 两球的加速度大小均为g•sinθ | |
| B． | Q球的加速度为零 | |
| C． | P球的加速度大小为2g•sinθ | |
| D． | P球的加速度方向沿斜面向上，Q球的加速度方向沿斜面向下 |
16．
物理学中有些问题的结论不一定必须通过计算才能验证，有时只需通过一定的分析就可以判断结论是否正确．如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环，两圆环上的电荷量均为q（q＞0），而且电荷均匀分布．两圆环的圆心O1和O2相距为2a，联线的中点为O，轴线上的A点在O点右侧与O点相距为r（r＜a）．试分析判断下列关于A点处电场强度大小E的表达式（式中k为静电力常量）正确的是（ ）
物理学中有些问题的结论不一定必须通过计算才能验证，有时只需通过一定的分析就可以判断结论是否正确．如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环，两圆环上的电荷量均为q（q＞0），而且电荷均匀分布．两圆环的圆心O1和O2相距为2a，联线的中点为O，轴线上的A点在O点右侧与O点相距为r（r＜a）．试分析判断下列关于A点处电场强度大小E的表达式（式中k为静电力常量）正确的是（ ）| A． | E=|$\frac{kq{R}_{1}}{{[R}_{1}^{2}+（a+r）^{2}]}$-$\frac{kq{R}_{2}}{[{R}_{2}^{2}+（a-r）^{2}]}$| | |
| B． | E=|$\frac{kq{R}_{1}}{[{{R}_{1}}^{2}+（a+r）^{2}]^{\frac{3}{2}}}$-$\frac{kq{R}_{2}}{[{R}_{2}^{2}+（a-r）^{2}]^{\frac{3}{2}}}$] | |
| C． | E=|$\frac{kq（a+r）}{{[R}_{1}^{2}+（a+r）^{2}]}$-$\frac{kq（a-r）}{[{R}_{2}^{2}+（a-r）^{2}]}$| | |
| D． | E=|$\frac{kq（a+r）}{[{R}_{1}^{2}+（a+r）^{2}]^{\frac{3}{2}}}$-$\frac{kq（a-r）}{[{R}_{2}^{2}+（a-r）^{2}]^{\frac{3}{2}}}$| |
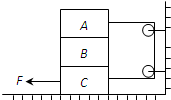如图所示，质量分别为mA=$\frac{1}{2}$mB=$\frac{1}{3}$mC=1kg的A、B、C三物体叠放在粗糙的水平地面上，各物体间及C物体与地面间的动摩擦因数均为μ=0.1．不计滑轮和绳的质量及其摩擦，若要用力将C物体匀速抽出，则所需拉力的最小值为8N．
