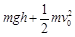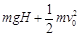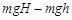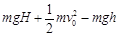题目内容
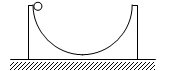
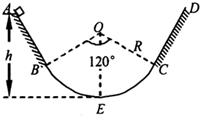
如图所示，在竖直平面内固定一半径R为2 m、圆心角为120°的光滑圆弧轨道BEC，其中点E是最低点．在B、C两端平滑、对称地连接长度S均为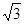
m的AB、CD两段粗糙直轨道，直轨道上端A、D与最低点E之间的高度差h均为2.5 m．现将质量为0.01 kg的小物块由A点静止释放，物块与直轨道间的动摩擦因数均为0.25．求：
(1) 小物块从静止释放到第一次过E点时重力做的功；
(2) 小物块第一次通过E点时的动能大小；
(3) 小物块在E点时受到支持力的最小值．
m的AB、CD两段粗糙直轨道，直轨道上端A、D与最低点E之间的高度差h均为2.5 m．现将质量为0.01 kg的小物块由A点静止释放，物块与直轨道间的动摩擦因数均为0.25．求：(1) 小物块从静止释放到第一次过E点时重力做的功；
(2) 小物块第一次通过E点时的动能大小；
(3) 小物块在E点时受到支持力的最小值．
(1) 0.25J(2) 0.23J(3) 0.2N
(1) 小物块从静止释放到第一次过E点时重力做的功WG=mgh=0.25J 2分
（2）根据动能定理：mghμmgscos600=Ek 2分 得Ek=0.23J 2分
（3）根据动能定理：mg(R-Rcos600)=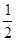
mv2 2分
由向心力公式有：FN-mg=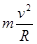
2分
得 FN=2mg=0.2N 2分
（2）根据动能定理：mghμmgscos600=Ek 2分 得Ek=0.23J 2分
（3）根据动能定理：mg(R-Rcos600)=
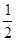mv2 2分由向心力公式有：FN-mg=
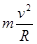2分得 FN=2mg=0.2N 2分
练习册系列答案
名校课堂系列答案
相关题目
