题目内容
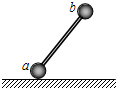 (2011?洪山区模拟)如图所示,一轻杆两端分别固定a、b两个半径相等的光滑金属球,a球质量大于b球质量.整个装置放在光滑的水平面上,将此装置从图示位置由静止释放,则( )
(2011?洪山区模拟)如图所示,一轻杆两端分别固定a、b两个半径相等的光滑金属球,a球质量大于b球质量.整个装置放在光滑的水平面上,将此装置从图示位置由静止释放,则( )分析:整个装置下落过程中,水平方向没有外力,水平方向的动量守恒.原来系统水平方向的动量为零,在b球落地前瞬间,系统水平方向的动量仍为零,a的速度一定为零.根据动量定理分别分析杆对b球水平方向的冲量和竖直方向冲量,再确定杆对b球的冲量.a球原来速度为零,b落地瞬间速度仍为零,根据动能定理分析杆对a做功为零.在b球下落过程中,系统的机械能守恒,根据守恒条件分析杆对a球和b球做功关系,确定轻杆对b球做的功.
解答: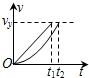 解:
解:
A、B、对两球及杆系统,在b球落地前瞬间,b球的水平速度为零,根据系统水平方向动量守恒,系统初始动量为零,则此时a球的速度必定为零,故A、B均错误;
C、对b球,水平方向上动量变化为零,由动量定理可知,杆对b球的水平冲量为零.在竖直方向上,根据系统机械能守恒可知,b落地时速度与只在重力作用下的速度一样,如图所示v-t图象中斜线为b球自由落体运动的图线,曲线为b球竖直方向的运动图线,在竖直方向上运动的位移与落地速度相同,对比可知b球落地所用时间相对自由落体运动的时间要长,由动量定理可知杆对b球的竖直方向的冲量必定不为零,且冲量方向向上,所以杆对b球的水平和竖直冲量可知,杆对b球的冲量不为零,且方向竖直向上.故C错误;
D、设杆对a球做功W1,对b球做功W2,系统机械能守恒,则除了重力之外的力的功必定为零,即W1+W2=0,对a球由动能定理可知W1=0,故W2=0.故D正确.
故选D.
 解:
解:A、B、对两球及杆系统,在b球落地前瞬间,b球的水平速度为零,根据系统水平方向动量守恒,系统初始动量为零,则此时a球的速度必定为零,故A、B均错误;
C、对b球,水平方向上动量变化为零,由动量定理可知,杆对b球的水平冲量为零.在竖直方向上,根据系统机械能守恒可知,b落地时速度与只在重力作用下的速度一样,如图所示v-t图象中斜线为b球自由落体运动的图线,曲线为b球竖直方向的运动图线,在竖直方向上运动的位移与落地速度相同,对比可知b球落地所用时间相对自由落体运动的时间要长,由动量定理可知杆对b球的竖直方向的冲量必定不为零,且冲量方向向上,所以杆对b球的水平和竖直冲量可知,杆对b球的冲量不为零,且方向竖直向上.故C错误;
D、设杆对a球做功W1,对b球做功W2,系统机械能守恒,则除了重力之外的力的功必定为零,即W1+W2=0,对a球由动能定理可知W1=0,故W2=0.故D正确.
故选D.
点评:本题是动量定理、动量守恒定律与机械能守恒定律的综合应用,难点在于分析轻杆对b球的冲量.利用作图法是分析物体运动常用方法.

练习册系列答案
相关题目

 (2011?洪山区模拟)如图所示,在光滑的水平面上,有一质量M=3kg的薄板和一质量m=1kg的物块朝相反方向运动,初速度大小都为v=4m/s,它们之间有摩擦.当薄板的速度大小为2.4m/s时,物块的运动情况是( )
(2011?洪山区模拟)如图所示,在光滑的水平面上,有一质量M=3kg的薄板和一质量m=1kg的物块朝相反方向运动,初速度大小都为v=4m/s,它们之间有摩擦.当薄板的速度大小为2.4m/s时,物块的运动情况是( ) (2011?洪山区模拟)如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=20m.由于传送带足够粗糙,假设选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立刻以a=2m/s2恒定向右的加速度跑至传送带最右端.
(2011?洪山区模拟)如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=20m.由于传送带足够粗糙,假设选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立刻以a=2m/s2恒定向右的加速度跑至传送带最右端.