题目内容
18.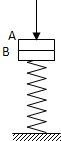 两个质量均为m的物体A、B叠放在一个直立的轻弹簧上,弹簧的劲度系数为K.今用一个竖直向下的力压物块A,使弹簧又缩短了△L(仍在弹性限度内),当突然撤去压力时,求A对B的压力是多大?
两个质量均为m的物体A、B叠放在一个直立的轻弹簧上,弹簧的劲度系数为K.今用一个竖直向下的力压物块A,使弹簧又缩短了△L(仍在弹性限度内),当突然撤去压力时,求A对B的压力是多大?
分析 先根据受力平衡求出弹簧的弹力,撤去F后,对AB整体运用牛顿第二定律求出加速度,再隔离A,运用牛顿第二定律求出B对A的作用力,进而根据牛顿第三定律即可求解.
解答 解:未加压力时对AB整体,由平衡条件得:
KL=2mg ①
突然撤去压力时对AB整体,由牛顿第二定律得:
K(L+△L)-2mg=2ma ②
对A由牛顿第二定律得:
N-mg=ma ③
解得B对A的支持力为:
$N=mg+\frac{k△L}{2}$ ④
由牛顿第三定律得A对B的压力也是 $mg+\frac{k△L}{2}$
答:A对B的压力是$mg+\frac{k△L}{2}$.
点评 本题主要考查了牛顿第二定律的直接应用,注意整体法和隔离法在题目中的应用.

练习册系列答案
相关题目
8.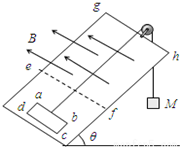 如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为L1,bc边的边长为L2,线框的质量为m,电阻为R,线框通过绝缘细线绕过光滑的滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为L1,bc边的边长为L2,线框的质量为m,电阻为R,线框通过绝缘细线绕过光滑的滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
 如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为L1,bc边的边长为L2,线框的质量为m,电阻为R,线框通过绝缘细线绕过光滑的滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为L1,bc边的边长为L2,线框的质量为m,电阻为R,线框通过绝缘细线绕过光滑的滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )| A. | 线框进入磁场前运动的加速度为$\frac{Mg-mgsinθ}{m}$ | |
| B. | 线框进入磁场时匀速运动的速度为$\frac{(Mg-mgsinθ)R}{B{l}_{1}}$ | |
| C. | 线框进入磁场时做匀速运动的总时间为$\frac{{B}^{2}{{l}_{1}}^{2}{l}_{2}}{(Mg-mgsinθ)R}$ | |
| D. | 该匀速运动过程产生的焦耳热为(Mg-mgsinθ)L2 |
9.用电磁式打点计时器记录自由落体运动的运动信息,并由此测量出自由下落的物体的下落的加速度,下列器材中,不需要的是( )
| A. | 6v学生交流电源 | B. | 纸带 | C. | 重锤和刻度尺 | D. | 秒表 |
6.关于位移和路程,下列说法错误的是( )
| A. | 物体通过的路程为零,但位移可能不为零 | |
| B. | 物体通过的位移不为零,那么路程一定不为零 | |
| C. | 物体沿直线向某一方向运动,通过的路程等于位移的大小 | |
| D. | 物体通过的几段路程不等,但位移可能相等 |
8.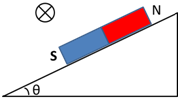 如图所示,条形磁铁放在倾斜桌面上,在其上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向内的电流,则( )
如图所示,条形磁铁放在倾斜桌面上,在其上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向内的电流,则( )
 如图所示,条形磁铁放在倾斜桌面上,在其上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向内的电流,则( )
如图所示,条形磁铁放在倾斜桌面上,在其上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向内的电流,则( )| A. | 磁铁对桌面压力减小,可能受到桌面的摩擦力作用 | |
| B. | 磁铁对桌面压力减小,一定受到桌面的摩擦力作用 | |
| C. | 磁铁对桌面压力增大,可能受到桌面的摩擦力作用 | |
| D. | 磁铁对桌面压力增大,一定受到桌面的摩擦力作用 |
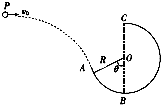 如图所示,一个质量m=0.6kg的小球以某一初速度从P点水平抛出,恰好沿光滑圆弧轨道ABC的A点的切线方向进入轨道(不计空气阻力).已知圆弧轨道的半径R=0.3m,θ=60°,小球到达A点时的速度v=4m/s,取g=10m/s2.
如图所示,一个质量m=0.6kg的小球以某一初速度从P点水平抛出,恰好沿光滑圆弧轨道ABC的A点的切线方向进入轨道(不计空气阻力).已知圆弧轨道的半径R=0.3m,θ=60°,小球到达A点时的速度v=4m/s,取g=10m/s2.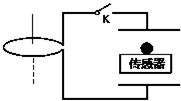 如图所示,两块金属板水平放置,与左侧水平放置的线圈通过开关K用导线连接.压力传感器上表面绝缘,位于两金属板间,带正电的小球静置于压力传感器上,变化的磁场沿线圈的轴向穿过线圈.K未接通时传感器的示数为1N,K闭合后传感器的示数稳定为2N.则磁场的变化情况可能是(设磁场向上为正方向)( )
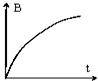
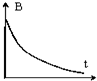
如图所示,两块金属板水平放置,与左侧水平放置的线圈通过开关K用导线连接.压力传感器上表面绝缘,位于两金属板间,带正电的小球静置于压力传感器上,变化的磁场沿线圈的轴向穿过线圈.K未接通时传感器的示数为1N,K闭合后传感器的示数稳定为2N.则磁场的变化情况可能是(设磁场向上为正方向)( )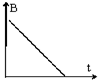

 如图所示,水平传送带AB的右端与在竖直面内的用内径光滑的钢管弯成的“9”形固定轨道相接,钢管内径很小.传送带的运行速度v0=4.0m/s,将质量m=1kg的可看做质点的滑块无初速地放在传送带的A端.已知传送带长度L=4.0m,离地高度h=0.4m,“9”字全高H=0.6m,“9”字上半部分圆弧半径R=0.1m,滑块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,试求:
如图所示,水平传送带AB的右端与在竖直面内的用内径光滑的钢管弯成的“9”形固定轨道相接,钢管内径很小.传送带的运行速度v0=4.0m/s,将质量m=1kg的可看做质点的滑块无初速地放在传送带的A端.已知传送带长度L=4.0m,离地高度h=0.4m,“9”字全高H=0.6m,“9”字上半部分圆弧半径R=0.1m,滑块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,试求: