题目内容
13.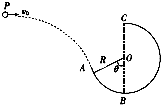 如图所示,一个质量m=0.6kg的小球以某一初速度从P点水平抛出,恰好沿光滑圆弧轨道ABC的A点的切线方向进入轨道(不计空气阻力).已知圆弧轨道的半径R=0.3m,θ=60°,小球到达A点时的速度v=4m/s,取g=10m/s2.
如图所示,一个质量m=0.6kg的小球以某一初速度从P点水平抛出,恰好沿光滑圆弧轨道ABC的A点的切线方向进入轨道(不计空气阻力).已知圆弧轨道的半径R=0.3m,θ=60°,小球到达A点时的速度v=4m/s,取g=10m/s2.(1)求小球做平抛运动的初速度v0的大小.
(2)求P点与A点间的水平距离x和竖直距离h.
(3)若已知小球到达圆弧轨道最高点C时的速度vC=$\sqrt{7}$m/s,求此时小球对轨道的压力NC.
分析 (1)恰好从光滑圆弧ABC的A点的切线方向进入圆弧,说明到到A点的速度vA方向与水平方向的夹角为θ,这样可以求出初速度v0;
(2)平抛运动水平方向做匀速直线运动,竖直方向做自由落体运动,根据平抛运动的基本规律求出P点与A点的水平距离和竖直距离;
(3)在C点,重力和弹力的合力提供向心力,根据向心力公式和牛顿第二定律列式求出小球在最高点C时对轨道的压力.
解答 解:(1)小球到A点的速度如图所示,由图可知
v0=vx=vAcosθ=4×cos60°=2m/s
(2)根据平抛运动的分运动公式,有:
${v}_{y}={v}_{A}sinθ=4×sin60°=2\sqrt{3}m/s$
由平抛运动规律得:
${v}_{y}^{2}=2gh$
vy=gt
x=v0t
h=0.6m
x=0.4$\sqrt{3}$m≈0.69m
(3)由圆周运动向心力公式得:
${N}_{C}+mg=m\frac{{v}_{C}^{2}}{R}$
代入数据得:
NC=8N
由牛顿第三定律得:小球对轨道的压力大小:
NC′=NC=8N,方向竖直向上
答:(1)小球做平抛运动的初速度v0为2m/s;
(2)P点与A点的水平距离为0.69m,竖直高度为0.6m;
(3)小球到达圆弧最高点C时vC=$\sqrt{7}$m/s,对轨道的压力为8N.
点评 本题是平抛运动和圆周运动相结合的典型题目,除了运用平抛运动和圆周运动的基本公式外;本题第三问中C点速度可以利用动能定理求解出来.

练习册系列答案
相关题目
3. 如图所示表示两列同频率相干水波在t=0时刻的叠加情况,图中实线表示波峰,虚线表示波谷,已知两列波的振幅均为1cm,波速为2m/s,波长为0.2m,下列说法正确的是 ( )
如图所示表示两列同频率相干水波在t=0时刻的叠加情况,图中实线表示波峰,虚线表示波谷,已知两列波的振幅均为1cm,波速为2m/s,波长为0.2m,下列说法正确的是 ( )
 如图所示表示两列同频率相干水波在t=0时刻的叠加情况,图中实线表示波峰,虚线表示波谷,已知两列波的振幅均为1cm,波速为2m/s,波长为0.2m,下列说法正确的是 ( )
如图所示表示两列同频率相干水波在t=0时刻的叠加情况,图中实线表示波峰,虚线表示波谷,已知两列波的振幅均为1cm,波速为2m/s,波长为0.2m,下列说法正确的是 ( )| A. | B、D两点是振动加强点,且位移始终处于最大 | |
| B. | A、C点是振动减弱点 | |
| C. | B、D两点在该时刻的竖直高度差为2 cm | |
| D. | t=0.025 s时刻A点距平衡位置2 cm |
4.下列关于时间与时刻、位移与路程的说法,正确的是( )
| A. | 1分钟有60个时刻 | |
| B. | 位移的大小永远不等于路程 | |
| C. | 物体通过一段路程,但位移可能为零 | |
| D. | 描述运动时,时刻对应的是一段位移,时间对应的是某一位置 |
1.下述关于力的说法正确的是( )
| A. | 力是物体对物体的作用,总是成对出现的 | |
| B. | 只有相互接触的物体间才有力的作用 | |
| C. | 有的物体自己就有力,这个力不需要其他的物体施加 | |
| D. | 力可以离开物体而独立存在 |
8.物体做初速度为零的匀加速直线运动,前2s内的位移是8m,则( )
| A. | 物体的加速度是2m/s2 | B. | 物体的加速度是4m/s2 | ||
| C. | 物体第2s末的速度是8m/s | D. | 物体第2s末的速度是4m/s |
2.初速度v0水平抛出一物体,当竖直分位移与水平分位移相等时,下列说法中不正确的是( )
| A. | 竖直分速度等于水平分速度 | B. | 瞬时速度为$\sqrt{5}$v02 | ||
| C. | 运动时间为$\frac{2{v}_{0}}{g}$ | D. | 速度变化方向在竖直方向上 |
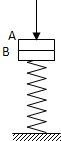 两个质量均为m的物体A、B叠放在一个直立的轻弹簧上,弹簧的劲度系数为K.今用一个竖直向下的力压物块A,使弹簧又缩短了△L(仍在弹性限度内),当突然撤去压力时,求A对B的压力是多大?
两个质量均为m的物体A、B叠放在一个直立的轻弹簧上,弹簧的劲度系数为K.今用一个竖直向下的力压物块A,使弹簧又缩短了△L(仍在弹性限度内),当突然撤去压力时,求A对B的压力是多大?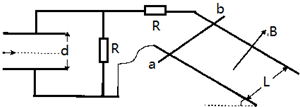 如图所示,质量为m1=0.2kg的导体棒ab,垂直放在相距为L=0.5m的平行光滑金属轨道上.导轨平面与水平面的夹角为θ=30°,并处于磁感应强度大小为B=2T、方向垂直与导轨平面向上的匀强磁场中,导轨足够长.左侧是水平放置、间距为d=0.1m、板长为2d、的平行金属板,图中两个电阻的阻值均为R=4Ω,不计其他电阻,g=10m/s2.释放导体棒,当棒沿导轨匀速下滑后,求:
如图所示,质量为m1=0.2kg的导体棒ab,垂直放在相距为L=0.5m的平行光滑金属轨道上.导轨平面与水平面的夹角为θ=30°,并处于磁感应强度大小为B=2T、方向垂直与导轨平面向上的匀强磁场中,导轨足够长.左侧是水平放置、间距为d=0.1m、板长为2d、的平行金属板,图中两个电阻的阻值均为R=4Ω,不计其他电阻,g=10m/s2.释放导体棒,当棒沿导轨匀速下滑后,求: 如图所示,两个重20N的相同物块A、B叠放在一起,受到l0N的水平推力Fl的作用,在水平地面上一起做匀速直线运动,则此时A受到的摩擦力等于0;若将B与 A并列,并让它们一起在同一水平地面上匀速前进,那么需要的水平推力F2等于F1.(填“大于”、“小于”或“等于”)
如图所示,两个重20N的相同物块A、B叠放在一起,受到l0N的水平推力Fl的作用,在水平地面上一起做匀速直线运动,则此时A受到的摩擦力等于0;若将B与 A并列,并让它们一起在同一水平地面上匀速前进,那么需要的水平推力F2等于F1.(填“大于”、“小于”或“等于”)