题目内容
图1为验证牛顿第二定律的实验装置示意图。图中打点计时器的电源为50Hz的交流电源,打点的时间间隔用Δt表示。在小车质量未知的情况下,某同学设计了一种方法用来研究“在外力一定的条件下,物体的加速度与其质量间的关系”。
(1)完成下列实验步骤中的填空:
①平衡小车所受的阻力:小吊盘中不放物块,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列________的点。
②按住小车,在小吊盘中放入适当质量的物块,在小车中放入砝码。
③打开打点计时器电源,释放小车,获得带有点迹的纸带,在纸带上标出小车中砝码的质量m。
④按住小车,改变小车中砝码的质量,重复步骤③。
⑤在每条纸带上清晰的部分,每5个间隔标注一个计数点。测量相邻计数点的间距s1,s2,…。求出与不同m相对应的加速度a。
⑥以砝码的质量m为横坐标, 为纵坐标,在坐标纸上做出
为纵坐标,在坐标纸上做出 关系图线。若加速度与小车和砝码的总质量成反比,则
关系图线。若加速度与小车和砝码的总质量成反比,则 与m处应成_________关系(填“线性”或“非线性”)。
与m处应成_________关系(填“线性”或“非线性”)。
(2)完成下列填空:
(ⅰ)本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是_______________________。
(ⅱ)设纸带上三个相邻计数点的间距为s1、s2和s3。a可用s1、s3和Δt表示为a=__________。图2为用米尺测量某一纸带上的s1、s3的情况,由图可读出s1=__________mm,s3=__________。由此求得加速度的大小a=__________m/s2。
(ⅲ)图3为所得实验图线的示意图。设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为___________,小车的质量为___________。
(1)①等间距 ⑥线性
(2)(ⅰ)远小于小车和砝码的总质量 (ⅱ) ,24.2,47.3,1.16 (ⅲ)
,24.2,47.3,1.16 (ⅲ)
解析试题分析:(1)①当平衡了摩擦力后小车的合力为0,给小车一个初速度后,小车做匀速运动,所以打下的点迹是等间距的。⑥据牛顿第二定律F=ma可得, ,当F一定是,
,当F一定是, 与m成正比,所以它们的关系是呈线性变化的。(2)ⅰ设吊盘和吊盘中砝码质量之和为m,小车的总质量为M,则有: mg=(M+m)a,
与m成正比,所以它们的关系是呈线性变化的。(2)ⅰ设吊盘和吊盘中砝码质量之和为m,小车的总质量为M,则有: mg=(M+m)a, ,当M>>m时,a=
,当M>>m时,a=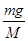 。ⅱ应用逐差法可得:s3-s1=2aT2=2a(5Δt)2,所以有a=
。ⅱ应用逐差法可得:s3-s1=2aT2=2a(5Δt)2,所以有a= ,读数分别是24.2、47.3mm,加速度大小求得:a=1.16m/s2。ⅲ据该图像中斜率k=
,读数分别是24.2、47.3mm,加速度大小求得:a=1.16m/s2。ⅲ据该图像中斜率k=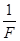 ,所以F=
,所以F= ;图线与纵轴的截距为b,则有
;图线与纵轴的截距为b,则有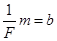 即
即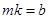 ,所以
,所以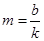 。
。
考点:本题考查验证牛顿第二定律中a与m的关系。

在研究“物体加速度与力的关系”的实验中,某学习小组使用的实验装置如图所示。轨道木板水平放置,把小车从位移传感器(接收器)旁边释放后,传感器能记录任意时刻小车的位置,据此可求得小车的加速度。(钩码的质量为 m,重力加速度为g)
(1)指出该实验中的一个明显疏漏___ 。
(2)某次实验中,依据传感器的记录,在时间t内,小车由静止开始发生的位移为x则小车的加速度的表达式为a=___________。
(3)纠正了疏漏之处后,保持小车(包含发射器)的总质量为M不变,通过多次实验,依据得到的数据,在a—F图象中描点(如图所示)。结果发现右侧若干个点明显偏离直线,造成此误差的主要原因是:
| A.小车与轨道之间存在摩擦 | B.导轨保持了水平状态 |
| C.所挂钩码的总质量太大 | D.所用小车的质量太大 |
为了“探究加速度与力、质量的关系”,请思考探究思路并回答下列问题:
(1)为了消除小车与水平木板之间摩擦力的影响应采取做法是___________
| A.将不带滑轮的木板一端适当垫高,使小车在钩码拉动下恰好做匀速运动 |
| B.将不带滑轮的木板一端适当垫高,使小车在钩码拉动下恰好做匀加速运动 |
| C.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动 |
| D.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀加速运动 |

(3)消除小车与水平木板之间摩擦力的影响后,可用钩码总重力代替小车所受的拉力,此时钩码m与小车总质量M之间应满足的关系为_______________;
(4)在“探究加速度与力的关系”时,保持小车的质量不变,改变小桶中砝码的质量,该同学根据实验数据作出了加速度a与合力F图线如图,该图线不通过坐标原点,试分析图线不通过坐标原点的原因.
答: .

某同学在竖直悬挂的弹簧下加挂钩码,探究弹力与弹簧伸长量的关系.上表是该同学的实验数据.实验时弹簧始终未超过弹性限度。g取10m/s2。
| 砝码质量m×10-3 kg | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长度l×10-2 m | 6.0 | 7.2 | 8.3 | 9.5 | 10.6 | 11.8 |

(2) 根据图象得到弹簧的劲度系数是______N/m.(结果保留2位有效数字)


 。
。 )(下图长度单位:m)
)(下图长度单位:m)
 ;
; ;
;

 某研究性学习小组为了制作一种传感器,需要选用一电器元件.图为该电器元件的伏安特性曲线,有同学对其提出质疑,先需进一步验证该伏安特性曲线,实验室备有下列器材:
某研究性学习小组为了制作一种传感器,需要选用一电器元件.图为该电器元件的伏安特性曲线,有同学对其提出质疑,先需进一步验证该伏安特性曲线,实验室备有下列器材: