题目内容
1. 如图所示工人在推一台重300N的割草机,其推力为F=100N,方向与水平面夹角为37°斜向下.(取g=10m/s2)
如图所示工人在推一台重300N的割草机,其推力为F=100N,方向与水平面夹角为37°斜向下.(取g=10m/s2)(1)割草机对地面向下的作用力是多少?
(2)地面与割草机的摩擦因数不应超过多少?(滑动摩擦力近似等于最大静摩擦力)
分析 (1)以割草机为研究对象受力分析,由竖直方向平衡求得地面对割草机的支持力,由牛顿第三定律得到割草机对地面向下的作用力;
(2)能够正常割草,则推力的水平分量要大于等于地面与割草机间的摩擦力,由此分析即可.
解答 解:(1)以割草机为研究对象受力分析有: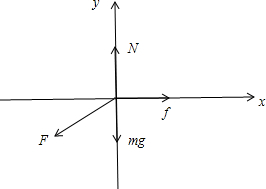
割草机在竖直方向受力平衡有:N-mg-Fsin37°=0
可得地面对割草机的支持力N=mg+Fsin37°=300+100×0.6N=360N
根据牛顿第三定律可知,割草机对地面向下的压力N′=N=360N;
(2)由上图分析可知,要保证割草机正常工作,则满足:
Fcos37°≥f
又f=μN
由以上两式可解得:$μ≤\frac{2}{9}$
答:(1)割草机对地面向下的作用力是360N;
(2)地面与割草机的摩擦因数不应超过$\frac{2}{9}$.
点评 本题是共点力平衡问题,运用三角函数法求解是常用的方法,基础是正确分析受力情况,由平衡条件得到拉力的表达式.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.作用于同一点的两个力大小分别为F1=10N,F2=6N,这两个力的合力F与F1的夹角为θ,则θ可能为( )
| A. | 0° | B. | 30° | C. | 60° | D. | 120° |
12.人造卫星在离地心为r的圆轨道上做匀速圆周运动,地球质量为M,地球半径为R,人造卫星质量为m,人造卫星绕地球的角速度为ω,万有引力恒量为G,地球表面重力加速度为g,计算人造卫星所受的向心力的式子正确的是( )
| A. | mg | B. | $\frac{GMm}{{{{(R+r)}^2}}}$ | C. | mω2R | D. | $\frac{{mg{R^2}}}{r^2}$ |
9. 在检测某款电动车性能的实验中,让电动车由静止开始沿平直的公路行驶,利用仪器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出如图所示的F-$\frac{1}{v}$图象,其中线段AB与$\frac{1}{v}$轴平行,线段BC的延长线过原点(C点为实线与虚线的分界点).假设电动车行驶中所受的阻力恒定,取重力加速度g=10m/s2.则( )
在检测某款电动车性能的实验中,让电动车由静止开始沿平直的公路行驶,利用仪器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出如图所示的F-$\frac{1}{v}$图象,其中线段AB与$\frac{1}{v}$轴平行,线段BC的延长线过原点(C点为实线与虚线的分界点).假设电动车行驶中所受的阻力恒定,取重力加速度g=10m/s2.则( )
 在检测某款电动车性能的实验中,让电动车由静止开始沿平直的公路行驶,利用仪器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出如图所示的F-$\frac{1}{v}$图象,其中线段AB与$\frac{1}{v}$轴平行,线段BC的延长线过原点(C点为实线与虚线的分界点).假设电动车行驶中所受的阻力恒定,取重力加速度g=10m/s2.则( )
在检测某款电动车性能的实验中,让电动车由静止开始沿平直的公路行驶,利用仪器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出如图所示的F-$\frac{1}{v}$图象,其中线段AB与$\frac{1}{v}$轴平行,线段BC的延长线过原点(C点为实线与虚线的分界点).假设电动车行驶中所受的阻力恒定,取重力加速度g=10m/s2.则( )| A. | 电动车所受阻力为2000N | B. | 电动车所受阻力为400N | ||
| C. | 电动车的额定功率为6 kW | D. | 电动车的最大速度为15 m/s |
16.已知某单色光的波长为λ,在真空中的光速为c,普朗克常量为h,则该单色光的能量子为( )
| A. | $\frac{hc}{λ}$ | B. | $\frac{hλ}{c}$ | C. | $\frac{h}{λ}$ | D. | hcλ |
13.关于电流的下列说法中,正确的是( )
| A. | 电路中的电流越大,表示通过导体横截面的电量越多 | |
| B. | 在相同时间内,通过导体截面的电量越多,导体中的电流就越大 | |
| C. | 通电时间越长,电流越大 | |
| D. | 因为电流有方向,所以电流是矢量 |
9.正点电荷q放在电场中的某一点,受到的电场力为F,测得该点的场强为E,换取另一点电荷-2q时,该点的场强和点电荷受到的力分别是( )
| A. | -2E-2F | B. | 2E 2F | C. | E 2 F | D. | E-2F |
 如图所示,竖直平面内一与水平方向夹角θ=60°的杆上套一铁环,铁环质量为m、直径略大于杆的截面直径;水平轻绳一端连在铁环上,一端连在质量为2m的小球上,小球受到的拉力F与杆平行,铁环和小球都处于静止状态,重力加速度为g.求:
如图所示,竖直平面内一与水平方向夹角θ=60°的杆上套一铁环,铁环质量为m、直径略大于杆的截面直径;水平轻绳一端连在铁环上,一端连在质量为2m的小球上,小球受到的拉力F与杆平行,铁环和小球都处于静止状态,重力加速度为g.求: