��Ŀ����
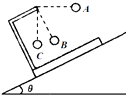
����Ŀ����ͼ��ʾ�����Ϊ37���б�泤L=1.82m����б������Ϸ���O�㽫һС�����ٶ�v0=3m/sˮƽ�׳������ͬʱ�ͷ���б�涥�˵Ļ��飬����һ��ʱ���С��ǡ�����Դ�ֱб��ķ�����л��飨С��ͻ��������Ϊ�ʵ㣬�������ٶ�g=10m/s2 �� sin37��=0.6��cos37��=0.8����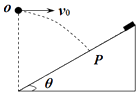
��1���׳���O��б��˵ĸ߶ȣ�
��2��������б���Ķ�Ħ�������̣�
���𰸡�
��1���⣺��С�����б��ʱ���ٶ�Ϊv����ֱ���ٶ�Ϊvy
���ԣ� ![]()
��С�������ʱ��Ϊt����ֱ����λ��Ϊy��ˮƽ����λ��Ϊx
vy=gt�� ![]() ��x=v0t
��x=v0t
�������ݵã�x=1.6m
���׳��㵽б����͵�ľ���Ϊh��h=y+xtan37��
���ϸ�ʽ������h=1.7m
���׳���O��б��˵ĸ߶�Ϊ1.7m��
��2���⣺��ʱ��t�ڣ������λ��Ϊs
���� ![]() ��
�� ![]()
mgsin37�㩁��mgcos37��=ma
�������������ݵã���=0.25
�𣺻�����б���Ķ�Ħ��������Ϊ0.25��
����������1������С��ǡ�����Դ�ֱб��ķ�����л��飬��С����ٶȽ��зֽ⣬�ٽ��С����ƽ�� �˶��Ĺ��ɽ�����⡣
��2����ʱ��t�ڣ��������ȱ����˶�����ţ�ٵڶ��������������б���Ķ�Ħ������
�����㾫�������û���Ħ�������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����Ħ����:���ù�ʽf=��F N ���м��㣬����FN ���������ѹ������һ������������������������ܺ�������.���߸���������˶�״̬������ƽ��������ţ�ٶ�������⣻�ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ��

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�