题目内容
6.已知地球半径为R,一单摆在山脚下(处于海平面高度,重力加速度为g)的周期为T,将该单摆移到高为h的山顶,其周期改变量△T为( )| A. | $\frac{R}{h}T$ | B. | $\frac{h}{R}T$ | C. | $\frac{R+h}{R}T$ | D. | $\frac{R}{R+h}T$ |
分析 根据万有引力和物体受到的重力的大小相等可以求得在地面上和高度为h处的重力加速度大小的表达式,进而由单摆的周期公式可以求得结果.
解答 解:设单摆的摆长为L,地球的质量为M.
据万有引力定律等于重力,得
在海平面上,有mg=$G\frac{Mm}{{R}^{2}}$,
在山顶上,有mg′=$G\frac{Mm}{{(R+h)}^{2}}$,
可得海平面的重力加速度和高度为H山顶上的重力加速度之比为:
g:g′=(R+h)2:R2;
据单摆的周期公式可知T=$2π\sqrt{\frac{l}{g}}$,
则得海平面上有:
T=$2π\sqrt{\frac{l}{g}}$,
山顶上有:
T+△T=$2π\sqrt{\frac{l}{g′}}$,
由以上各式可求得:
$△T=\frac{h}{R}T$,
故B正确,ACD错误.
故选:B.
点评 单摆的周期是由单摆的摆长和当地的重力加速度的大小共同决定的,在不同的地方,重力加速度的大小不同.

练习册系列答案
相关题目
17.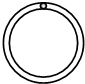 如图所示,一质量为0.5kg可以看成质点的小球,在竖直放置的光滑圆管轨道内运动,当小球以10m/s的速度通过圆管的最高点时,小球对圆管的压力大小为1N,如果小球以15m/s的速度通过圆的最高点时,对轨道的压力大小为 (重力加速度g=10m/s2)( )
如图所示,一质量为0.5kg可以看成质点的小球,在竖直放置的光滑圆管轨道内运动,当小球以10m/s的速度通过圆管的最高点时,小球对圆管的压力大小为1N,如果小球以15m/s的速度通过圆的最高点时,对轨道的压力大小为 (重力加速度g=10m/s2)( )
 如图所示,一质量为0.5kg可以看成质点的小球,在竖直放置的光滑圆管轨道内运动,当小球以10m/s的速度通过圆管的最高点时,小球对圆管的压力大小为1N,如果小球以15m/s的速度通过圆的最高点时,对轨道的压力大小为 (重力加速度g=10m/s2)( )
如图所示,一质量为0.5kg可以看成质点的小球,在竖直放置的光滑圆管轨道内运动,当小球以10m/s的速度通过圆管的最高点时,小球对圆管的压力大小为1N,如果小球以15m/s的速度通过圆的最高点时,对轨道的压力大小为 (重力加速度g=10m/s2)( )| A. | 13.5N | B. | 8.5N | C. | 9N | D. | 4N |
11.以下几种说法,正确的是( )
| A. | 因为空气分子间存在斥力,所以用气筒给自行车打气时,要用力才能压缩空气 | |
| B. | 用手捏面包,面包体积会缩小,这是分子间有间隙的缘故 | |
| C. | 打开酒瓶后可嗅到酒的气味,说明分子在做无规则的运动 | |
| D. | 把碳素墨水滴入清水中,观察到的布朗运动,是碳分子无规则运动的反映 |
15.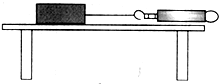 如图所示,在探究摩擦力的实验中,测力计与水平桌面平行,拉力从零逐渐增大,拉力为8N时,木块不动;拉力为12N时,木块恰好被拉动;木块匀速运动时拉力为10N.木块与桌面间的滑动摩擦力和最大静摩擦力分别是( )
如图所示,在探究摩擦力的实验中,测力计与水平桌面平行,拉力从零逐渐增大,拉力为8N时,木块不动;拉力为12N时,木块恰好被拉动;木块匀速运动时拉力为10N.木块与桌面间的滑动摩擦力和最大静摩擦力分别是( )
 如图所示,在探究摩擦力的实验中,测力计与水平桌面平行,拉力从零逐渐增大,拉力为8N时,木块不动;拉力为12N时,木块恰好被拉动;木块匀速运动时拉力为10N.木块与桌面间的滑动摩擦力和最大静摩擦力分别是( )
如图所示,在探究摩擦力的实验中,测力计与水平桌面平行,拉力从零逐渐增大,拉力为8N时,木块不动;拉力为12N时,木块恰好被拉动;木块匀速运动时拉力为10N.木块与桌面间的滑动摩擦力和最大静摩擦力分别是( )| A. | 12 N,8 N | B. | 12 N,10 N | C. | 10 N,12 N | D. | 10 N,8 N |
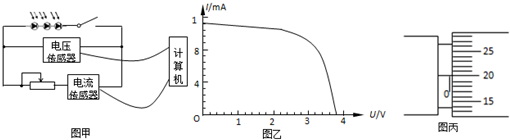
 在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: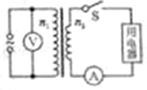 如图,将额定电压为60V的用电器,通过一理想变压器接在正弦交变电源上.闭合开关S后,用电器正常工作,交流电压表和交流电流表(均为理想电表)的示数分别为220V和2.2A.则变压器输入功率为132V,通过原线圈的电流的最大值为0.85A.
如图,将额定电压为60V的用电器,通过一理想变压器接在正弦交变电源上.闭合开关S后,用电器正常工作,交流电压表和交流电流表(均为理想电表)的示数分别为220V和2.2A.则变压器输入功率为132V,通过原线圈的电流的最大值为0.85A.